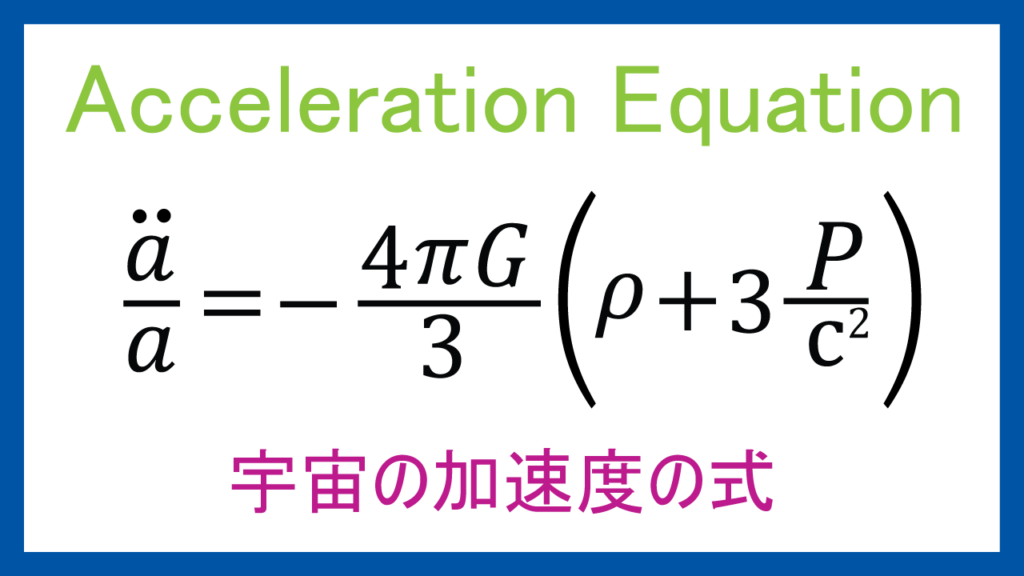
宇宙論を学んでいくために、フリードマン方程式とFluid Equationの2つの方程式を導出した。
どうやらもうひとつ大切な方程式が残っているようだ。
$$\frac{\ddot{a}}{a}=-\frac{4\pi G}{3}\bigg(\rho+3\frac{P}{c^2}\bigg)$$
これがその式で名前をAcceleration Equationという。
今回はその導出をやっていきたいのだが、使うのはこれまで導き出してきた2つの方程式が使われる。
まずはフリードマン方程式
$$ \left( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3} \rho -\frac{Kc^2}{a^2} $$
この両辺を時間\(t\)について微分してみる
$$2\bigg(\frac{\dot{a}}{a}\bigg)\bigg(\frac{\ddot{a}a-\dot{a}^2}{a^2}\bigg)=\frac{8\pi G}{3}\dot{\rho}+2\frac{kc^2}{a^3}\dot{a}$$
次はFluid Equationを使う
$$\dot{\rho}+3\frac{\dot{a}}{a}\bigg(\rho + \frac{P}{c^2}\bigg)=0$$
これを
$$\dot{\rho}=-3\frac{\dot{a}}{a}\bigg(\rho + \frac{P}{c^2}\bigg)$$
と整理して、先ほどの時間微分したフリードマン方程式に組み込んでやると
$$\frac{\ddot{a}}{a}-\bigg(\frac{\dot{a}}{a}\bigg)^2=-4\pi G \bigg(\rho+\frac{P}{c^2}\bigg)+\frac{kc^2}{a^2}$$
となる。この左辺の2項目はオリジナルのフリードマン方程式の左辺と同じなので、それを代入してやると
$$\frac{\ddot{a}}{a}=-\frac{4\pi G}{3}\bigg(\rho+3\frac{P}{c^2}\bigg)$$
Acceleration Equationが得られる。
フリードマン方程式の左辺が宇宙空間の距離的なものを表すスケール因子(\(a\))の時間微分だったので空間の広がりの速度的なものであると認識したけれども、今回得られたAcceleration Equationの左辺は名前の通り、スケール因子を2階時間微分したものとなっていて、宇宙の広がりの加速度(Acceleration)を表しているのだろう。
右辺を見てみると括弧の中に物質に関する密度\(\rho\)と圧力\(P\)があり、それらが万有引力定数\(G\)と掛け合わさせる。それにマイナスの符号が付いているので物質が存在し引力が増えると、宇宙が広がる加速度がマイナスになるということだ。
これが、昔宇宙が最終的には縮んで一点に収縮してしまうと考えられていた理由だろう。宇宙が広がっていると天文学者のハッブルが発見してからも、宇宙には物質があり、どうやら目に見えない質量を持ったダークマターも想像以上に宇宙に存在しているようだと理解されていたので、上のAcceleration Equationからも、宇宙は収縮するだろうと考えるのは当然のことであった。(僕も最初混乱したけれども、宇宙の広がりの加速度がマイナスだからと言ってすぐさま宇宙の大きさが小さくなるというわけではない。広がるスピードが減速するのであって、宇宙のサイズが小さくなり始めるのは、広がるスピードがゼロになってからである。)
しかしその後、またもやハッブルの名を冠する宇宙望遠鏡が、今度は宇宙が「加速しながら」広がっていることが確認された。これは宇宙に散らばるダークマターなどから発生する引力を凌駕する逆向きの力が働いていることを意味している。科学者はその力を持つ正体不明のエネルギーをダークエネルギーと呼ぶことにした。
話をAcceleration Equationに戻そう。
この方程式のおもしろいところは、これまでフリードマン方程式に存在していた空間の曲率\(k\)がなくなっていることである。
ちなみにここではできるだけシンプルなモデルを考えているので、その他の細かい力の影響は考えられていない。
これで3つの重要な方程式が出そろった。これらがどのように宇宙の表現に使われるのかが楽しみだ。
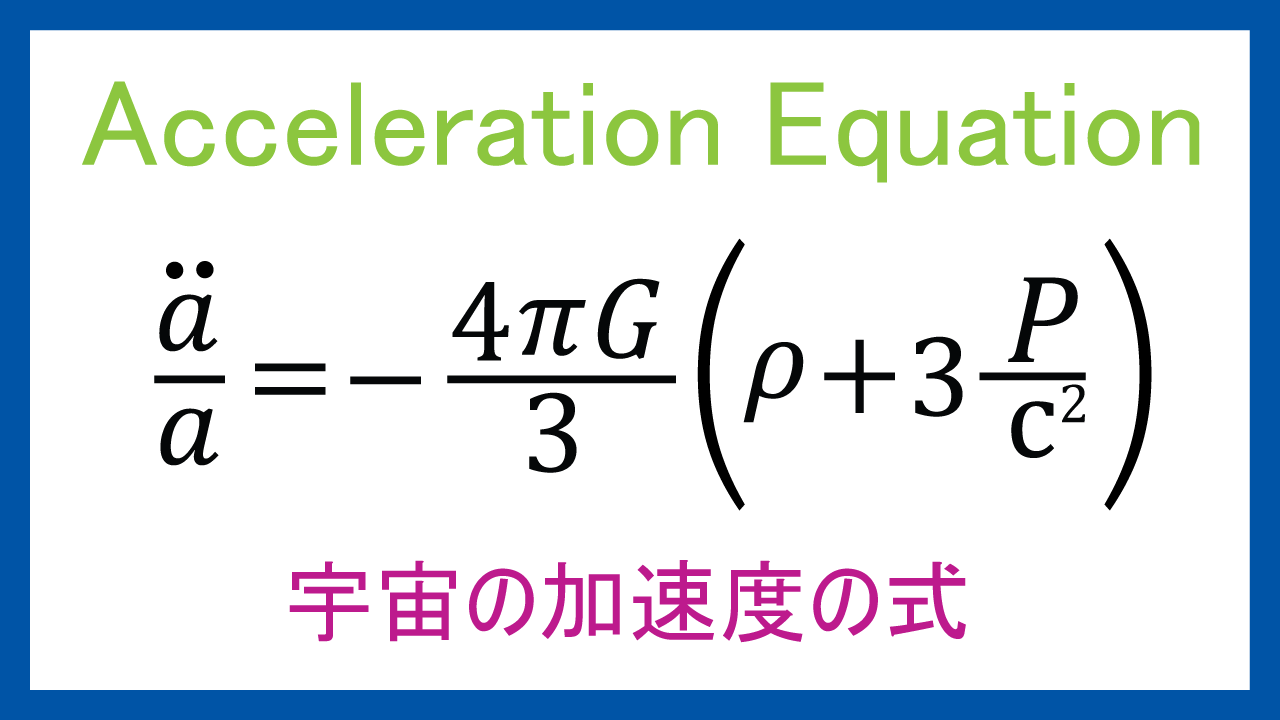



コメント