宇宙の年齢を計算してみよう

目的：ハッブルの法則を使って宇宙の年齢を計算する。

宇宙を学んでいると、ハッブルという名前がたくさん出てくる。

ハッブルというのは人の名前だ。彼は天文台を使って、宇宙が広がっていることを発見した張本人である。宇宙は静止していると信じていたアインシュタインは、宇宙が静止するように宇宙に関する方程式に”ある操作”を加えたのだが、ハッブルの発見により「あれ（方程式の操作）は人生最大の失敗だった」と言わしめることとなった。この方程式に関することは、また別の機会に取り上げてみることにしよう。

天文台で宇宙を観測していたハッブルは、遠くにある星ほど速いスピードで地球から離れて行っていることを発見した。それに関するグラフがこれだ。

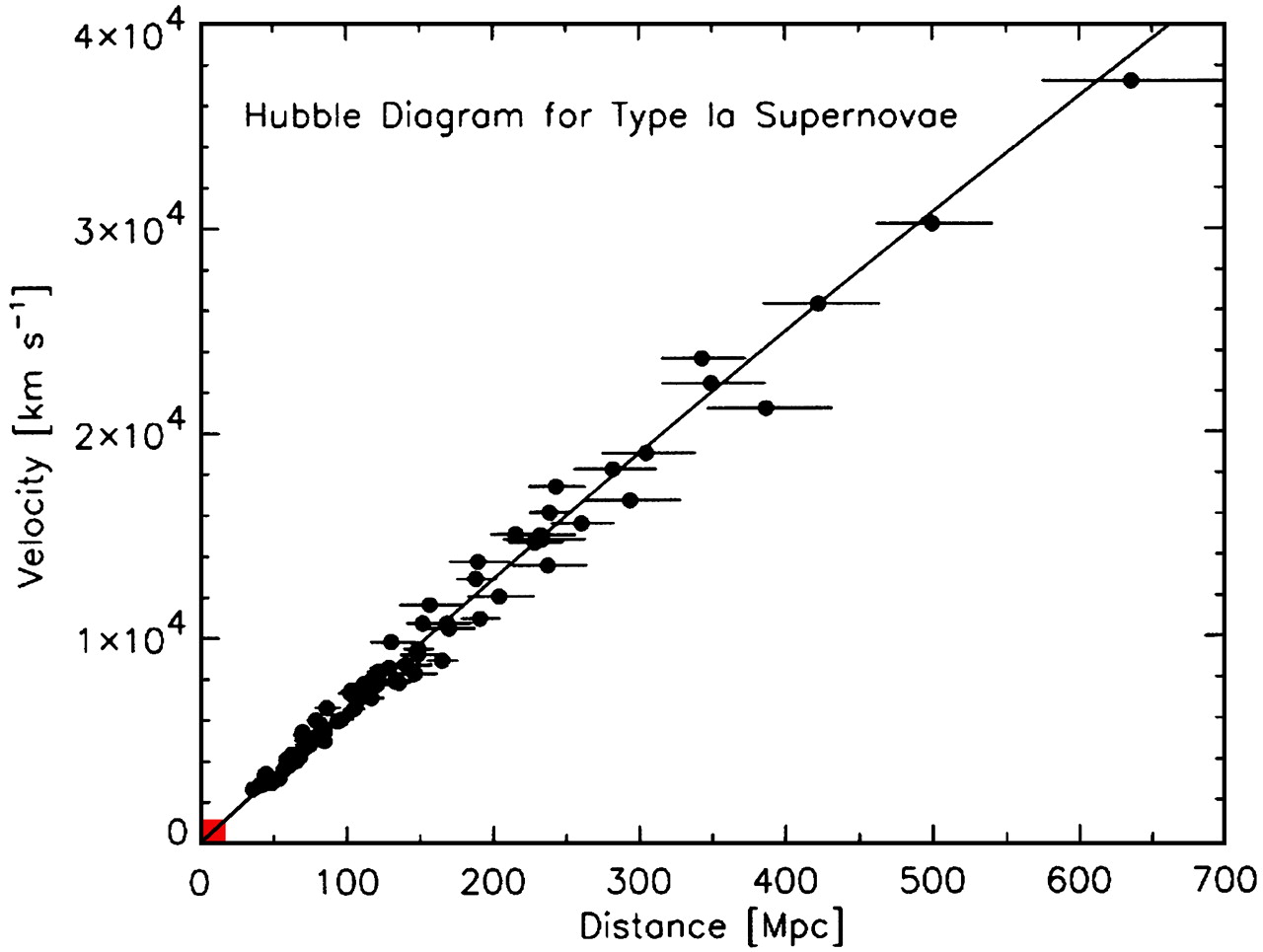
黒い点はそれぞれ星を表していて、横の軸を「それぞれの星と地球との距離」、縦の軸を「それぞれの星が地球から遠ざかる速さ」を示している。このグラフから、星がグラフの右側にあるほど（地球からの距離が離れているほど）、その星はよりグラフの上に位置している（より速いスピードで地球から離れて行っている）ことがわかる。

このようにきれいに一直線に並んだグラフは、簡単な数式で表すことができる。

$$v=H\times r$$

日本語に言い換えれば、

$「その星が地球から遠ざかる速さ」＝　H（ハッブル定数）×　「その星と地球との距離」$

ということになる。この直線における傾きが $H（ハッブル定数）$となっている。

現在、そのハッブル定数は大体$70.5km/(s・Mpc)$となっているらしい。ここで$「Mpc」$って何ぞや？と思うかもしれないけど、これは言ってしまえば長さだ。メガパーセクと呼び、メートルに直すと$3.09×10^{22} m$となる。何でこんなまどろっこしいことをするのかというと、メートルという単位は宇宙を扱うにはいささか短すぎるのだろう。

その$「Mpc」$をメートルに変えてやると、分母と分子の距離の単位（mとkm）が消え、ハッブル定数の単位を$1/s$に直すことができる

$$H=70.5\frac{km}{s・Mpc}\times \frac{1000m}{km}\times \frac{Mpc}{3.09 \times 10^{22}m}=2.28 \times 10^{-18} (\frac{1}{s})$$

これで単位が$1/s$となった、これは時間の逆数（分子と分母をひっくり返したもの）ということである。でもよくよく考えれば、当たり前のことなのである。

例えば、車のスピードを式で表してみよう。そうすると
$$車の速さ＝\frac{これまで進んだ距離}{これまでかかった時間}$$
と表すことができる。分数になっているので分かりづらいかもしれないけれど、かけ算を使って少しアレンジをするともう少しわかりやすくなるかもしれない。

$$車の速さ＝\frac{1}{これまでかかった時間}\times これまで進んだ距離$$

これならどうだろうか、真ん中にある分数の分母は時間なので単位は$1/s$となる。そうするとやっていることは、ハッブル定数の入った式$v=H\times r$の計算と同じなのである。ハッブル定数などという小洒落たものが入っているけども、実際は車の速さを計算する式と同じようなものだ。厳密には違うと思う、なぜなら僕たちの周りの天体が自ら進んで距離を伸ばしていると考えるよりも、宇宙全体が膨張しているために地球と天体の距離が離れて行っていると考える方が良いそうだ。

ただ、ハッブル定数の単位が$1/s$ということから、大まかな考え方で、それを逆数にしてやれば、天体が進んだにしろ、宇宙が広がったにしろ、大体のこれまでにかかった時間がわかるのではないかという推測がたつ。実際、計算してみるとうまくいきそうだ。先ほど単位を$1/s$に揃えてやったハッブル定数の逆数をとり、単位を$Year$に変えてみよう。

$$\frac{1}{H} \frac{s}{1}×\frac{min}{60s}×\frac{hour}{60mins}×\frac{day}{24hours}×\frac{Year}{365days}$$

$$=1.39×10^{10}Years となる、これは139億年のことである。$$

実際は、宇宙は加速しながら膨張しているらしいので、この数値よりもう少し小さな値になるようだ。137億年だったか。ただ、考え方としては意外とシンプルだと思う。宇宙の膨張を加速と捉えず、膨張速度が一定だと仮定して、ハッブル定数を少しいじってやるだけで大体の宇宙の年齢を計算することができたのだった。

世の中にはよく知らないだけで、知ってしまえば「なーんだそういうことか」となるものが多いのではないかと思う。周りには、新しいことをやるときに怖がらせる人が多すぎる。友だちや家族、会社の人をついつい怖がらせていないだろうか。僕も知らないうちに、新しくチャレンジする心の芽を摘んでしまっているかもしれない。そうはならないようにしよう。本当に難しいのなら、その人自身で体験してもらいたいし、難しくてもその人の能力や環境には適しているかもしれない。そんなことだれにもわからないのだ。どうせなら、そういった人たちの背中を押す存在になりたいと思う。

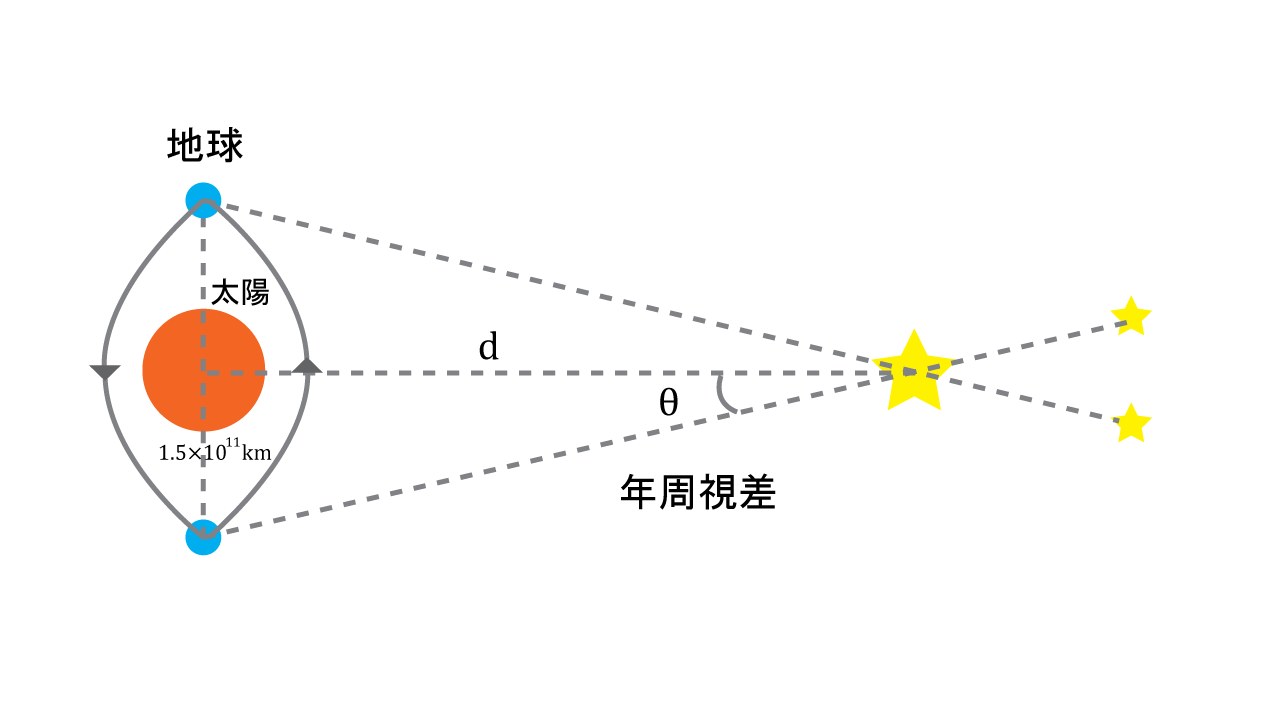
そもそも天体の距離はどうやって測るのか疑問に感じられた方は下の記事をご覧になってください。