はじめに
物理を学んだことのない人も、この式だけは知っているかもしれない。
$$E=mc^2$$
ご存知、アインシュタインの式だ。あのホーキング博士も一般読者向けに出す本を書くときに、知り合いに「数式がひとつ増えるたびに売り上げが半減する」と言われ、できるだけ数式を書かないようにしたらしいのだが、唯一このアインシュタインのエネルギーと質量等価の式だけは省けなかった、という話を聞いたことがある。
こういう自分も、もともと理系ではなく社会学部という理系とは程遠いところで勉強していたし、高校でも物理の授業はなかったのだが、この方程式の存在だけは知っていた。当時から物理や数学というものに興味はあった。しかし、プロのサッカー選手になるため毎日やっていたことと言えばボールを蹴る練習だったし、なにより圧倒的な頭の回転速度の遅さに悩まされていたので、こんな自分が物理や数学を勉強するなんておこがましい、と諦めてしまっていたのだ。ちなみにプロのサッカー選手にはなれなかった。
それでも一般人向けの科学本などを読んでみたりしたものだ。するといろいろな本の中に、このアインシュタインの式が出てくる。「僕も理系だったらこの式の意味もわかるのかな」とうらやましく思っていた。その時は「また来世というものがあるのなら、そのときチャレンジしてみようかな」ぐらいの気持ちであったのだが、まさかここまで勉強できることになるとは思いもよらなかった。
おかげでキャリアや安定といった状態とは無縁の生活を送ることになっているのだが、10年越しに自分の知りたかったことが何となくでも理解できるようになって、個人的にはとても満足している。
しかし驚いたことと言えば、物理学生として再び大学生になったとき、このアインシュタインの式を計算で使うことはあっても、この式がどのようにして導き出されるのかは教えてもらわなかったことだ。まぁ誰でも入れるような控えめな大学に行ったので、レベルがそんなに高くなかったからかもしれないが、少し残念に思った。
この\(E=mc^2\)がどうやって導出できるのかを理解したのは、その控えめな、人生2つ目の大学を物理専攻として卒業後、自分自身で特殊相対性理論を勉強してからだ。授業の課題やテストに追われることなく、自分のペースで勉強を始めてから多くのことを学んだ。時間のない中で、課題やテストの準備をしようとするとどうしても内容や式の理解よりもテクニックに走ってしまう。それは自分の勉強不足だったし、頭が悪いからだ。そういったものに追われることなく勉強したのはいいが、一応少し前まで理系の学生であったのに、その当時は全然物理を理解していなかったんだな思うと少し情けないなと感じる。
プライベートな話が多くなってしまったが、それだけ特別な感情が相対性理論にはあるし、本に頼りながらでも、このアインシュタインの式が自分の手から導き出されたときは、ちょっとばかり感動したものだ。物理をやってきてよかったなと思った瞬間だ。
この感動をわかりやすく伝えられるようになれたらいいなと思う。僕はかなり遠回りをしてきたけど、もう少し僕なりに近道を教えていきたい。わかりにくいところや、厳密には正しくない説明や表現があるかもしれない。しかし僕のような素人が物理を楽しむ上では十分だ。細かいところに気がいき過ぎて全体が見れなかったり、立ち止まってしまっては元も子もない。もちろん僕の解釈レベルや説明能力が上がってきたら、その都度編集していくつもりだ。あたたかい目で見守っていただきたい。
特殊相対性理論
\(E=mc^2\)は相対性理論から出てくる式なんだけども、その中でも特殊相対性理論という部類に入る理論だ。相対性理論には特殊相対性理論と一般相対性理論に分かれていて、なじみのない人にはSpecial(特殊)と書かれてある特殊相対性理論の方が特別感があって難しそうと思うかもしれないが、実はGeneral(一般)相対性理論の方がもっと難しい。「特殊」というのは「限定された状況下の中だけで成り立つ」という意味の「特殊」である。いつも日常で使われている言葉の感覚とは違うかもしれない。
どのように違うのかは、ここでは横に置いておこう。つまりは特殊相対性理論の方が簡単なのだ。
とりあえず、「(光以外の)全ては相対的である」“相対性原理”と「光の速さが慣性系によらず一定」“光速度一定の原理”という2つの原理をつじつま合わせて理論を組み立てられたものという認識を持とう。
簡単に言えば力学と電磁気学を「光の速さはどんな時も一緒」という原則を侵さない様に合体させたのである。個人的には、この表現を使うのは物理の初心者にはわかりづらいと思うのだが、なにせ本当のことだから仕方がない。この表現の意味が後々になって理解できると考えた方が良いかもしれない。頭の隅に入れておいてほしい。
光の進む距離が変わる
前回用いた(一定速度で動く)大きな部屋をもう一度考えよう。
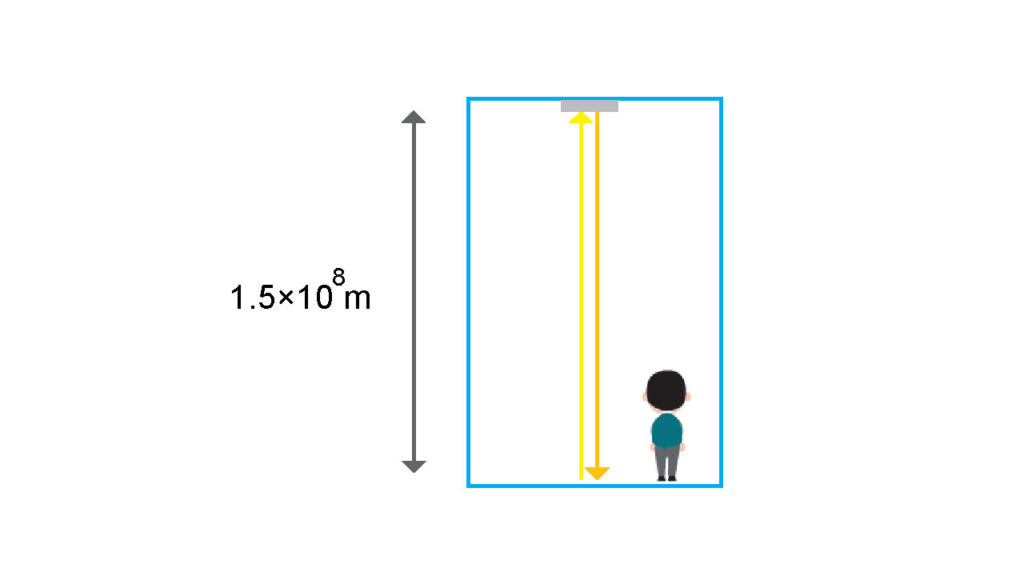
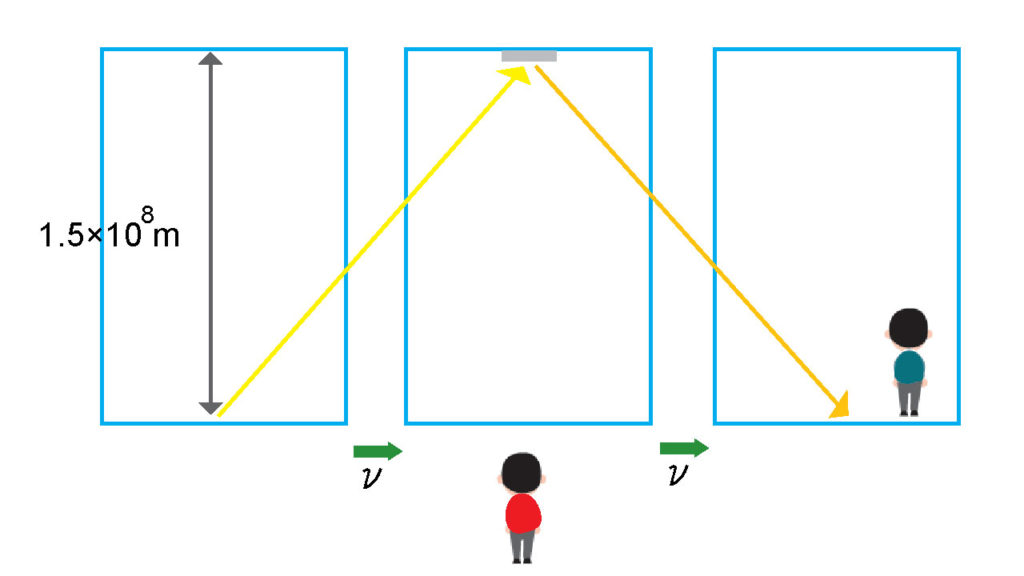
光が天井の鏡に向かって発射され、ちょうど1秒かかって元に戻ってくるような大きな部屋が地面に水平に\(v\)という速度で動いている。動いている部屋の中で青い人が見る光の軌道と、地面に立っている赤い人の見る光の軌道は違っている。明らかに赤い人が見る光の軌道の方が長くなっている。
ここで「光速度不変の原理」を壊さないように、このように動いている部屋と動いていないでいる場所、それぞれの関係性をどのように表せばいいのか。結論を先に言ってしまえば、ローレンツ係数と呼ばれるものを式に組み込むことで矛盾が解消されることになる。その導き方は、この下に書くことにする。
もう少し一般化していえば、(一定速度で)動いている系と動いていない系(別の慣性系)の間で光速度不変の原理を適応させるという話である。ちなみにその動いている系が加速しているときは特殊相対性理論の範囲外。さっき「限定された状況下の中で成り立つ」と言ったのはこのことだ。加速している系を扱うのは、もっとややこしい話になるので一般相対性理論の中で取り扱われることになる。
ローレンツ係数\(\gamma\)
光速度不変の原理を維持したまま、一定速度で動いている系と動いていない系の関係性を表すにはローレンツ係数が必要だということを言ったがまず、このような三角形を考えよう。
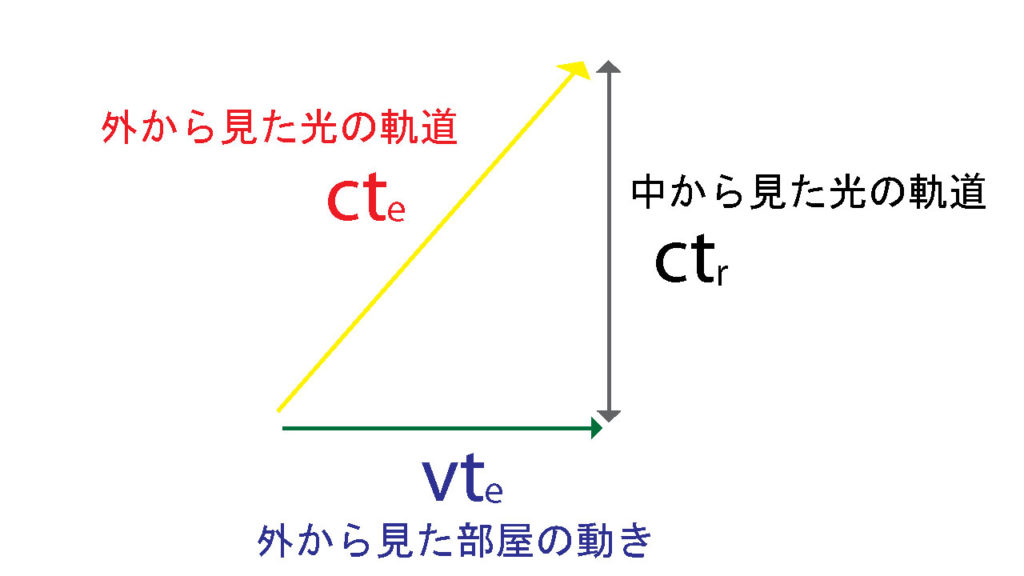
部屋の外から見た黄色い光の軌跡を\(ct_e\)で表す。それは光の速さで進んでいるので光速\(c\)を使った。さらに時間を表す\(t\)に下付きの\(e\)を付けたのは、その大きな部屋の外にいる赤い人は地球\(earth\)に立っていると仮定したからである。 言うまでもないが、\(速さ×時間=距離\)なので単位は全て距離を表している。
緑の矢印は、地球の地面に立っているその赤い人が見た大きな部屋の動いた距離である。部屋は\(v\)という速さで動いていて、それには地球の赤い人が感じる時間なので、同じく\(t_e\)を使っている。
縦の灰色の矢印は、部屋の中の青い人が見る光の軌跡である。光速度不変の原理により\(c\)を区別せずそのまま使い、今回は部屋\(room\)の中ということで\(t_r\)を用いる。
ピタゴラスの定理により
$$(ct_r)^2=(ct_r)^2+(vt_e)^2$$
同じ種類の\(t\)を左右で揃えて
$$(ct_r)^2=(ct_e)^2-(vt_e)^2$$
$$(ct_r)=\sqrt{(ct_e)^2-(vt_e)^2}$$
$$t_r=\frac{\sqrt{(ct_e)^2-(vt_e)^2}}{c}$$
\(c=\sqrt{c^2}\)なので
$$t_r=\sqrt{\frac{(ct_e)^2-(vt_e)^2}{c^2}}$$
$$=\sqrt{(t_e)^2-\frac{(vt_e)^2}{c^2}}$$
$$=t_e\sqrt{1-\frac{v^2}{c^2}}$$
\(t_r\)と\(t_e\)を入れ替えて
$$t_e=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}t_r$$
ここで\(\gamma=\frac{1}{\sqrt{1-v^2/c^2}}\)とおくと
$$t_e=\gamma t_r$$
となる。この\(\gamma=\frac{1}{\sqrt{1-v^2/c^2}}\)がローレンツ係数と呼ばれているものだ。速度を持つものの時間にローレンツ係数を掛け合わせると、光速度不変の原理をぶち壊すことなく、それぞれの時間を計算することができるのだ。光速\(c\)を区別せず、時間を2種類\((t_r, t_e)\)用意して計算した結果だ。
さらに計算してもらえればわかるけども、もしその大きな部屋が\(v=0.5c\)(光速の半分の速さ)で移動していたとすると、\(\gamma \approx 1.155\)となり、結果\(t_e=1.155 t_r\)となる。
もっとその部屋の速度が大きく\(v=0.8c\)だったとすれば\(t_e \approx 1.667 t_r\)となる。つまり、高速の\(8\)割で動く部屋の中で進む\(1\)秒の間に、\(1.667\)秒間地球では進むことになる。
部屋の動くスピードが速ければ速いほど、部屋の中に流れる時間がゆっくりになるのだ。
逆に、その部屋が光速に比べて無視できるほどの速度で進んでいた場合、\(\gamma=1\)となるので、\(t_e=t_r\)で時間の伸び縮みが確認できない。それは僕たちが普段生活している範囲内で起こる状況なので、これまでの力学と同じ考え方をすれば良いだけだ。こういった意味でも相対性理論はこれまでの力学を包括した理論といえる。言い方を変えれば、物体が光速に対して無視できないほどの速度で動いているならば、相対性理論を使わなくてはならない。
ローレンツ収縮
時間だけでなく物体の長さも変化する。動いているものの長さは\(\gamma=\sqrt{1-v^2/c^2}\)倍に縮むのだ。これをローレンツ収縮と呼ぶ。試しにその物体が光速の\(8\)割で進んでいたとしよう。すると\(\gamma\)の値は\(0.6\)になり、本来の長さの6割の長さになってしまう。
ちなみに、もし物体が光速と同じ速度(\(v=c\))で進むと\(\gamma\)の値は0になる。後でもう一度説明するが、これは光にとってはすべての長さが0にあることを意味している。
ところで、これまでの古典力学では3次元で物事を取り扱うことが多かったが、相対性理論ではそれらに時間軸を加えた4次元を使うことになる。厳密にいえば、時間に光速を掛け合わせたもの\(ct\)軸を3次元空間\((x, y, z)\)に加えるのだ。単位はどれも距離になるのでとりあえずは問題なさそうだ。
ミンコウスキー空間
ミンコウスキー空間とは特殊相対性理論で扱えるようにした4次元時空間。普段使っている3次元の空間に時間の次元を組み合わせたものだが、ただ軸を4本並べたものでは、光速度普遍の原理を反映できないので、ある種の工夫が必要になってくる。
その工夫をこしらえるのにあたって、先ほどのローレンツ係数がひとつのカギになってくる。動いているものの長さは\(\sqrt{1−v^2/c^2}\)倍に縮むとさっきチラッと説明したが、光がトンネルの中を進む状況を考えれば、光から見ると,トンネルが光速\(c\)で逆向きに動いているように見えるので,トンネルの長さは\(\sqrt{1−c^2/c^2}=\sqrt{1-1}=0\)倍,すなわち長さ\(0\) となってしまう。
もうひとつは、ベクトルの概念を応用してみるといい。ベクトルというと\(a(3,4)\)のように原点から延びる矢印のようなものをイメージすると思うが、このベクトルの矢印の長さ自体は、そのベクトルを座標の上を動かしたとしても変わらない。さらにピタゴラスの定理を知っていれば、そのベクトルの長さを表すことができる。
$$|a|=\sqrt{3^2 +4^2}=5$$
文字を使って、より一般的に書けば
$$|a|=\sqrt{x^2 +y^2}$$
これは3次元\((x,y,z)\)になっても同じく成り立つ。
$$|a|=\sqrt{x^2 +y^2 +z^2}$$
この調子でいけば、4次元\((x,y,z,ct)\)になってもすべての要素を2乗したものをルートの中に組み込んでやればベクトルの長さが与えられるはずだと予想できる。
$$|a|=\sqrt{x^2 +y^2 +z^2 +(ct)^2} $$
注意しなければならないが、この式はミンコウスキー空間では正しくない。ここで思い出してほしいのが、4次元の内3つは一般的な距離を示す次元(\(x,y,z\))を使ったけれども、もうひとつの次元は時間と光速を掛け合わした次元(\(ct\))を使っていたことだ。やはりもともと時間であったもの\(ct\)と、普段使いの距離たち\((x, y, z)\)を完全に同等なものとして扱うのはどうかと思われる。
そこで光から見ると、どんなものの長さも0になってしまうという結果をこの時空間(簡単のため2次元\(x\)と\(ct\))に適応させてみよう。
さっきどんな長さのトンネルも、光にとっては0になってしまうということで
\(\sqrt{1−c^2/c^2}=\sqrt{1-1}=0\) という計算をした。ということは、この2次元の時空の座標\((x,ct)\)の中で距離を計算しようとするのならば、ベクトルの長さの式\(|a|=\sqrt{x^2 + (ct)^2}\)の結果が0でなければならない。
$$ |a|=\sqrt{x^2 + (ct)^2}=0$$
という式が出るが、\(x\)も\(ct\)2乗にしてあるのに、正の数であるはずの2つの数の和が0になるのは気持ち悪いのでルートの中の演算はマイナスを使ってあげよう。すると
$$ |a|=\sqrt{x^2 – (ct)^2}=0$$
これを4次元\((x, y, z, ct)\)に拡張してやると、そこでのベクトルの長さの式は
$$ |a|=\sqrt{x^2 + y^2 +z^2 -(ct)^2}$$
となるべきだ。これがミンコフスキー空間での長さを表す式となっている。
このように光速度不変の原理を取り込んだ4次元空間をミンコウスキー空間と呼ばれている。時間軸を距離的なものとして扱い3次元に組み込んだわけだが、時間軸\(ct\)だけ符号が違っているところをみると全く同じ次元として認識するのは怪しい考えなのかもしれない。
しかし、これで特殊相対性理論で使える座標が定まったのだ。
ローレンツ変換
簡単のために、もう一度\(y\)軸と\(z\)軸を省略して、2次元だけのミンコフスキー空間\((x, ct)\)を考えよう。ここではちゃんとグラフを描くぞ。
ミンコフスキー空間でグラフを描くときは、縦軸を\(ct\)軸、横軸を\(x\)軸と置く。
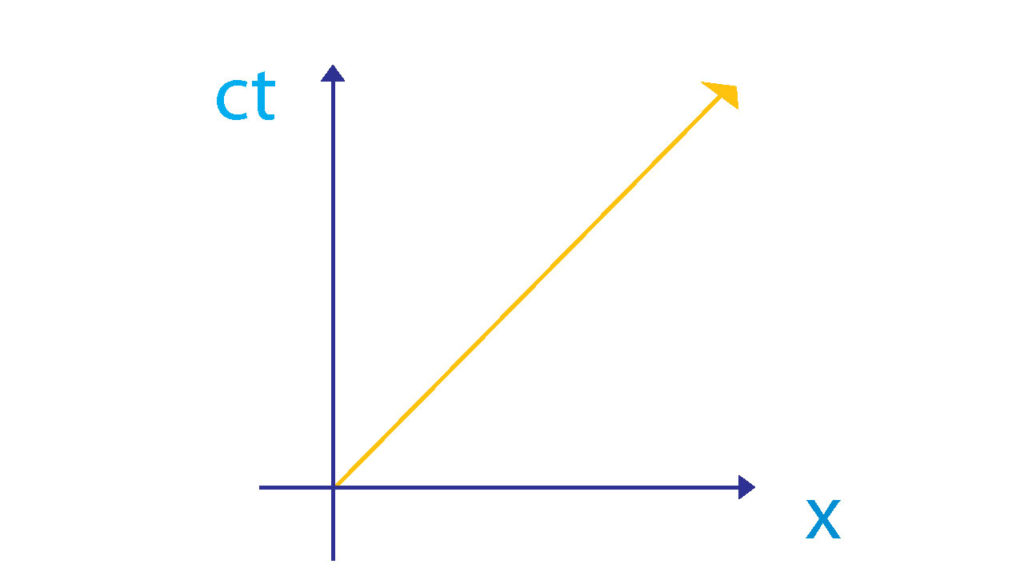
繰り返しになるが、縦の軸が\(ct\)になっているのは単位を距離に合わせるためである。 黄色の線は光の軌跡を示している。
もうひとつのミンコウスキー空間の特徴として、光の軌跡の傾きを1とするグラフで描かれてあることだ。数学的に書けば、光の速さを
$$c=\frac{x}{t}$$
と記述することである。いろいろな値を取りうる\(x\)や\(t\)と違って、光速を示す\(c\)は定数なので、それを1とすることで都合がよくなる。
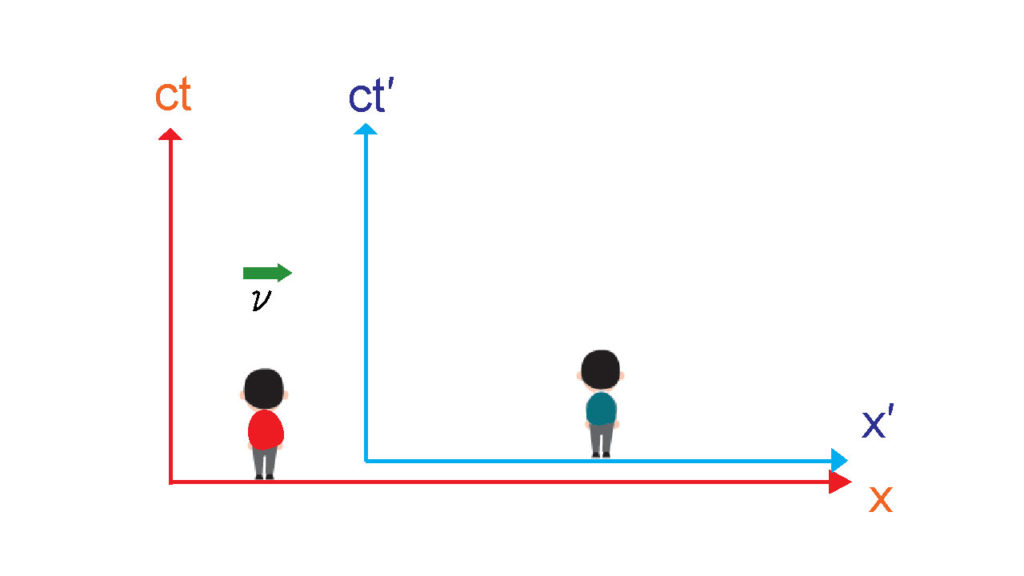
これを踏まえたうえで、一定速度で動いている系と動いていない系をミンコフスキー空間で描いてみよう。
動いていない系を先ほど図で表したように\((x, ct)\)、動いている系(さっきの例でいえば大きな部屋)を\((x’, ct’)\)を使うことにする。
そうして\(x’\)を\(x\)で表そうとすれば
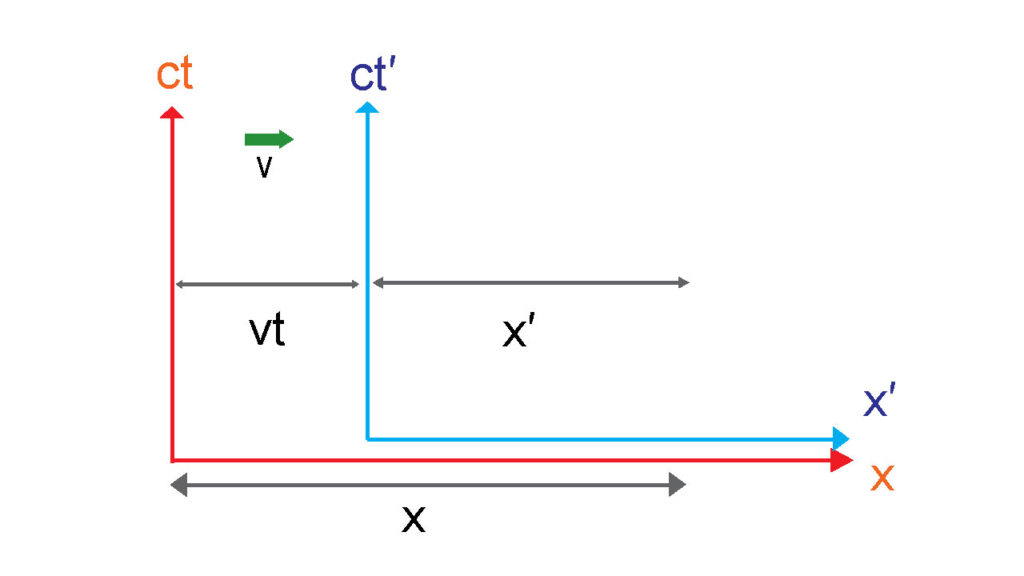
$$x’=x-vt$$
となる。しかし、特殊相対性理論では、これでは不十分なのである。先ほど説明した通り、距離に対してもローレンツ係数を考慮しなければならないので
$$x’=\gamma(x-vt)$$
と書くのがより一般的である。
ちなみに\(x’=x-vt\)と書くのは(光速度不変の原理を用いない)ガリレイ変換と呼ばれるもので、古典力学的な表現だ。
相対性理論では長さだけでなく時間も絶対的なものでないことを述べたが、動いている系の時間\(t’\)と動いていない系の時間\(t\)の関係はどのように書けるだろうか。
さきほどの\(x’=\gamma(x-vt)\)の両辺に\(c\)で割ってあげよう。
$$\frac{x’}{c}=\gamma (x-vt)/c$$
$$\frac{x’}{c}=\gamma (x/c-vt/c)$$
さらに右辺の2項目だけに\(c/c\)をかけ合わせると
$$\frac{x’}{c}=\gamma (x/c-vtc/c^2)$$
ここでミンコフスキー空間の特徴として\(t=x/c\)を紹介したことを思い出してほしい。このことから\(t’=x’/c\)でもあるし、\(x=ct\)でもある。これらを代入してやると
$$t’=\gamma (t-vx/c^2)$$
となる。
グラフには表記されていないが、ミンコフスキー空間では4次元の時空間について考えるものなので、本来は\(y\)軸と\(z\)軸についても議論されるべきなのだが、この例では大きな部屋は\(x\)軸に沿って平行に一定速度で動いているのを想定しているので、結局
$$y’=y$$
$$z’=z$$
となり、無視してよい結果となる。これが「簡単のために2次元のミンコフスキー空間\((x, ct)\)を考えよう」と初めに言った理由である。
まとめると
$$x’=\gamma (x-vt)$$
$$y’=y$$
$$z’=z$$
$$t’=\gamma (t-vx/c^2)$$
という変換式の集まりが、光速度不変の原理を壊さないように動いている座標と動いていない座標の変換式で、ローレンツ変換と呼ばれている。
どちらの座標をダッシュありと置くかどうかで右辺の符号が+になることもあるので、他のサイトや教科書ではちょっと違って見えるかもしれない。
このローレンツ変換があっているかどうか確かめる
特殊相対性理論では時間をひとつの次元として扱い、4次元空間(ミンコウスキー空間)を作り出していると説明した。そのミンコフスキー空間での長さを表す式
$$ |a|=\sqrt{x^2 + y^2 +z^2 -(ct)^2}$$
の両辺を2乗するとルートがはずれる
$$ a^2=x^2 + y^2 +z^2 -(ct)^2$$
ということはだ、動いている系の座標を表す\((x’, y’, z’, ct’)\)で表された
$$ a^2=x’^2 + y’^2 +z’^2 -(ct’)^2$$
も同じく成り立っていなければならない。ローレンツ変換を施してひとつ前の式に戻るのかどうか確かめよう。僕の計算を信じてもらえる人はこの計算部分を飛ばしてもらって構わない。
それぞれのダッシュ付き文字に代入すると
$$a^2=(\gamma(x-vt))^2 + y^2 + z^2 -(c(\gamma(t-vx/c^2)))^2$$
$$=\gamma^2 x^2 – 2\gamma^2 xvt + \gamma^2 v^2 t^2 + y^2 + z^2 -c^2\gamma^2 t^2 +2\gamma^2 xvt – \gamma^2 v^2 x^2/c^2$$
$$= \gamma^2 x^2- \gamma^2 v^2 x^2/c^2 + y^2 +z^2 +\gamma^2 v^2 t^2 – c^2 \gamma^2 t^2$$
$$= x^2(\gamma^2(1-v^2/c^2)) +y^2 +z^2 +\gamma^2 t^2(v^2-c^2)$$
右辺の第2項に\(c^2/c^2\)をかけると
$$= x^2(\gamma^2(1-v^2/c^2)) +y^2 +z^2 +\gamma^2 t^2 c^2(v^2/c^2-1)$$
$$= x^2(\gamma^2(1-v^2/c^2)) +y^2 +z^2 -\gamma^2 t^2 c^2(1-v^2/c^2)$$
ここで\(\gamma=\frac{1}{1-v^2/c^2}\)であるので
$$= x^2(\gamma^2/\gamma^2) +y^2 +z^2 -t^2 c^2(\gamma^2 /\gamma^2)$$
$$a^2= x^2 +y^2 +z^2 -c^2 t^2$$
というふうに、動かない座標(ダッシュなし文字)で表された式に戻すことができた。
2つの式の両辺は\(a^2\)という共有の文字が使われている。ということは
$$(一定)^2= x^2 +y^2 +z^2 -(ct)^2 = x’^2 + y’^2 +z’^2 -(ct’)^2 $$
となり、まるでデカルト座標において座標を回転させても、中心からの距離が一定だということを表す式に似ている。
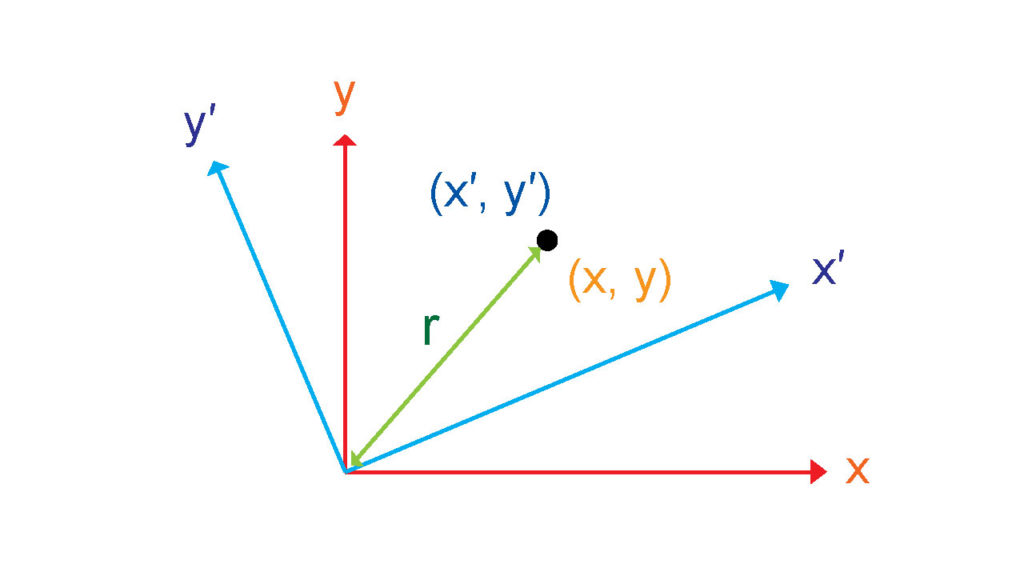
$$r^2= x^2 +y^2= x’^2 + y’^2$$
この事実から、ローレンツ変換は時空間の座標回転であると言うこともできる。相対性理論は座標変換の学問であることを感じられる部分であると思う。しかし相対性理論の神髄は一般相対性理論において重力を時空間の歪みと捉えることである。一般相対性理論に進むと座標変換のオンパレードである。専門用語を使って言えば、テンソルを使った計算をするのだが、これを書いている時点で僕にそれらを説明する能力は全くない。
4次元空間の不変量、固有時\(\tau\)
ミンコフスキー空間において、全ての項を式の片側に集めて2乗したものがどうやら不変量(一定)となるようだった。もう一度ここに書こう。
$$(一定)^2=x^2 +y^2+ z^2 -(ct)^2$$
ここで後の議論で簡単にするために空間と時間の符号を入れ替える。ミンコウスキー空間の説明のところで、それぞれの符号が逆になっているのは、光にとってはどんな長さも0になってしまうという計算結果の辻褄を合わせるためであった。
きちんと計算方法を書くとしよう。先ほど
$$ |a|=\sqrt{x^2 – (ct)^2}=0$$
としてあったのを、\(ct\)と\(x\)の順番を入れ替えて
$$ |a|=\sqrt{(ct)^2 – x^2}=0$$
とする。これを4次元に拡張させて
$$ |a|=\sqrt{(ct)^2 -x^2 -y^2 -z^2}$$
と書き換えることができる。
今、左辺はaとなっているが、アインシュタインは代わりに固有時\(\tau\)を導入し、
$$ \tau^2=\sqrt{(ct)^2 -x^2 -y^2 -z^2}$$
のように表した。座標軸を回転させただけの3次元の円の式の半径\(r\)の値が変わらないように、この固有時\(\tau\)も不変量になっているのだ。
ここでなぜこの不変量が固有時という時間に関係しているような名前になっているのかが疑問に思っている人もいると思う。ごもっともな疑問である。先ほど時間というのは絶対的な尺度でないと言ったところなのに!
ここからの議論でわかりやすくするために、それぞれの要素\((ct,x,y,z)\)の微小量を扱うということで、代わりに\((cdt,dx,dy,dz)\)を用いよう。文字の前にdを付けることは、微積分を少しかじったことのある人なら抵抗ないと思う。要はこれから微積分の計算のために、それぞれの要素を小さな変化量として考えるのだ。時間軸\(ct\)の\(c\)の前に微小変化の\(d\)が付いていないのは、光速度不変の原理により光速\(c\)はどんな場合も変化しないからだ。
ここでこのミンコウスキー空間で物体が移動しない場合を考えよう。移動しないということは、空間の三次元の要素\((dx,dy,dz)\)それぞれが0の場合である。
$$dx=dy=dz=0$$
これを先ほどの固有時の式に代入すると
$$(d\tau)^2=(cdt)^2-0-0-0$$
つまり
$$d\tau=cdt$$
となり、何となくこの\(\tau\)が時間に関係するような感じがしないでもない。実際この固有時を時間的なものとして扱うことで、4次元における速度を定義していくことになる。
4元速度
4次元空間で速度をどのように表せることができるだろうか
速度の公式は
$$速度=\frac{距離}{時間}$$
であるので、4次元分の速度を作ることができる。ここでの”時間”に固有時\(d\tau\)を用いる。
$$u^0=\frac{cdt}{d\tau}$$
$$u^1=\frac{dx}{d\tau}$$
$$u^2=\frac{dy}{d\tau}$$
$$u^3=\frac{dz}{d\tau}$$
と表すことができる。4元速度に使われている\(u\)の右肩に数字が付いているがそれらは指数ではない。相対性理論の流儀のようなものなので、文脈で判断する必要がある。
4次元におけるローレンツ係数
4元速度はイメージするのはなかなか難しいが、やっていることは何となく理解しやすい。しかし、その中でもちょっと気持ち悪いのがやはり時間軸\(ct\)方向の速度\(u^0\)だ。
なかなか捉えにくい概念であるが、少し式をアレンジしてやることで馴染みの顔が現れる。
もう一度固有時の式を記そう
$$ \tau^2=(ct)^2 -x^2 -y^2 -z^2$$
両辺に\(cdt\)で割ってやると
$$(\frac{d\tau}{cdt})^2 =1-(\frac{dx}{cdt})^2 -(\frac{dy}{cdt})^2 -(\frac{dz}{cdt})^2$$
$$(\frac{d\tau}{cdt})^2 =1-\frac{1}{c^2}\Big\{(\frac{dx}{dt})^2 -(\frac{dy}{dt})^2 -(\frac{dz}{dt})^2 \Big\}$$
\(\frac{dx}{dt}\)というのは、\(x\)方向の速度のことを表している。同じように\(\frac{dy}{dt}\)は\(y\)、\(\frac{dz}{dt}\)は\(z\)方向の速度であるので
$$=1-\frac{1}{c^2}(v^2_x +v^2_y +v^2_z)$$
\(v_x +v_y +v_z\)を\(\vec{v}\)とすれば
$$=1-\frac{1}{c^2}\vec{v^2} $$
よって
$$\frac{d\tau}{cdt}=\sqrt{1-\vec{v}^2/c^2} $$
さらにこれを逆数にしたものは
$$\frac{cdt}{d\tau}=u^0=\frac{1}{\sqrt{1-\vec{v}^2/c^2}}=\gamma$$
となり、4元速度の時間軸に対する速度がローレンツ係数に対応しているのがわかった。
ちなみに\(u^1\) \(u^2\) \(u^3\)も少し計算してやればローレンツ係数が浮かび上がってくる。
$$u^1=\frac{dx}{d\tau}=\frac{cdt}{d\tau}\frac{dx}{cdt}=\gamma \frac{dx}{cdt}=\frac{\gamma}{c}v_x$$
この計算を繰り返すことで
$$u^2=\frac{\gamma}{c}v_y$$
$$u^2=\frac{\gamma}{c}v_z$$
を得る。
4元運動量
これまで速度を4次元で解釈してきたのだが、他にも4次元にできるものは何だろうか。
せっかく4元速度を定義したのだから、質量×速度が運動量になるように、4元速度に質量をかけ合わせて4元運動量を作ってみよう。
しかし気を付けなければならないのが、4元速度を定義するとき普通の時間の代わりに固有時\(d\tau\)を分母に持ってきていたので、その割りすぎてしまった\(c\)に合わせて\(c\)をかけて調整しなければならない。物理で単位を揃えるのは基本中の基本だ。
物理を全くやってなかった文系時代に、何気なく理科の本を眺めているとき「そうや!単位を常に意識してやれば、どんな計算も上手くいきそうだ。僕はとんでもないテクニックを発見してしまったかもしれない!」と興奮したことがあったのだが、それが物理や数学を学んでいる人にとって、どんなに基本的な考えであるかわかるまでもう少し時間がかかった。
ともあれ
$$p^0=mcu^0$$
$$p^1=mcu^1$$
$$p^2=mcu^2$$
$$p^3=mcu^3$$
という4次元の運動量的なものが定義できたのである。4元速度に\(mc\)をかけただけである。
もう一度固有時の式を見てみよう
$$ (d\tau)^2=(cdt)^2 -(dx)^2 -(dy)^2 -(dz)^2$$
全ての次元の要素を2乗して片方の辺に集めることで不変量(この場合は固有時)を求めることができた。
4元速度もこの式の両辺に\((d\tau)^2\)で割ることによって
$$(\frac{d\tau}{d\tau})^2=(\frac{cdt}{d\tau})^2-(\frac{dx}{d\tau})^2-(\frac{dy}{d\tau})^2 – (\frac{dz}{d\tau})^2 $$
$$(\frac{d\tau}{d\tau})^2=(u^0)^2-(u^1)^2-(u^2)^2 – (u^3)^2 $$
そこで4元運動量を作るために両辺に\((mc)^2\)をかける
$$(mc)^2=(mcu^0)^2-(mcu^1)^2-(mcu^2)^2-(mcu^3)^2$$
$$(mc)^2=(p^0)^2-(p^1)^2-(p^2)^2-(p^3)^2$$
ここで先ほど計算した\(u^0=\gamma,\ u^1=\frac{\gamma}{c}v_x,\ u^2=\frac{\gamma}{c}v_y,\ u^3=\frac{\gamma}{c}v_z\)を使うと
$$p^0=\gamma mc,\ p^1=\gamma mv_x,\ p^2=\gamma mv_y,\ p^3=\gamma mv_z$$
なので
$$(mc)^2=(\gamma mc)^2-(\gamma mv_x)^2-(\gamma mv_y)^2-(\gamma mv_z)^2$$
と書き直すことができる。全ての項にローレンツ係数である\(\gamma\)が付いていて、いかにも特殊相対性理論を取り扱っているなという感じがする。時間や距離が伸び縮みするとき、光速度不変の原理を崩さないようにそれぞれにローレンツ係数を付けて計算するのであった。しかし動いている物体が光の速さに比べて無視できるぐらい遅い速度で動いている場合はローレンツ係数\(\gamma\)の値が1に近づくので、この係数の効果を無視して古典力学的な表現で問題なかった。
同じように、上の式にローレンツ係数が付いているが物体が低速で動いている状況を考え、ローレンツ係数を無視してみよう。
するとさっきの式は(\(p^0\)は\(\gamma mc\)というイマイチよくわからないものなので、そのままに置いておく。というか最終的にはp^0について解いて意味を確認する。)
$$(mc)^2=(p^0)^2-(p_x)^2-(p_y)^2-(p_z)^2$$
前に3次元空間の速度の合成\(v_x^2+ v_y^2+ v_z^2=\vec{v}^2\)と表したように
3次元空間の運動量を\(p_x^2+ p_y^2+ p_z^2=\vec{p}^2\)とすることで
$$(mc)^2=(p^0)^2-\vec{p}^2$$
不可解な\(p^0\)について解いてやると
$$p^0=\sqrt{(mc)^2+\vec{p}^2}$$
$$=mc\sqrt{1+\frac{\vec{p}^2}{(mc)^2}}$$
ここで\(x\)が限りなく0に近い小さな数のときに成り立つ近似式
$$f_{(x)}=(1+x)^n=1+nx+\frac{1}{2!}n(n-1)x^2+…$$
を用いると
$$p^0=mc(1+\frac{\vec{p}^2}{2(mc)^2}+…)$$
$$=mc+\frac{\vec{p}^2}{2mc}+…$$
\(p^0\)の単位は\(kg\ m/s\)なので、これに\(c(m/s)\)をかけると\(J(kg\ m^2/s^2)\)というエネルギーの単位になる。それを\(E\)と置いて
$$E=p^0c=mc^2+\frac{\vec{p}^2}{2m}+…$$
この物体が速度をもたない、つまり運動量も\(0\)\((\vec{p}=0)\)のとき右辺の2項目以降が0になるので
$$E=mc^2$$
と表すことができる。
これが質量とエネルギーが等価であるという有名なアインシュタインの式である。
まとめ
これが物理学でもっとも有名な方程式の導き方である。
といっても素人の自分がいろいろなものを参考にしながら書いたものなので、数学的厳密さなどに関しては全く自信がない。しかし大まかな流れは間違っていないだろうし、少し数学の知識があればアインシュタインを筆頭とする天才たちがが辿った思考の片りんを触れるぐらいには楽しめるものになったのではないだろうか。
厳密さを追求するがあまりに素人にとってわかりにくくなってしまったり、余計な一言や難しい表現のせいで学ぶことが嫌いになってしまうことはよくあることだ。できるだけそういう説明の仕方は省いて言ったつもりだが、まだまだわかりにくいところはあるので、そこは徐々に改善していきたいと考えている。
大まかにまとめると
・光の速さはどんなときも一定である、という原理を持ち込む。
・ミンコウスキー空間という4次元の時空間を設定する。
・その中でエネルギーというものを考えると\(E=mc^2\)という式が現れた。
という流れであった。
エネルギーと質量は等価であるという式の意味をただ単に教えてもらうより、それがどのような論理や計算を使って導出されたのかに興味があった。さまざまなソースに頼りながらとはいえ、自分の手でその方程式を導き出すことができたなら、小さいながらも達成感があるというものだ。
次の目標は、重力が時空間の歪みであるということを数学的に理解することである。きちんと説明できるということは、きちんと理解しているということ。できるだけ早く説明できるようになりたい。



コメント