ダークマターの発見

１９００年初頭、アインシュタインが相対性理論を発表してから間もないころは、宇宙が広がっているのか、縮んでいるのか、はたまた止まっているのかは全然わかっていなかった。

この後、ハッブルによって宇宙が広がっていることが観測によって証明されるのだが、それまではアインシュタインの一種の宗教的な考えから、宇宙は広がってもなければ、縮まってもいないという定常的な宇宙というものをイメージしていた。周りの科学者も「あのアインシュタインが言うのだから間違いないだろう」という感じで、同じような考えを持っていたようだ。

結局、１９２９年に望遠鏡を使った観測から「遠い星ほど地球から速い速度で遠ざかっている」というハッブルの法則を発表し、定常的な宇宙という考えが間違っていることを証明した。

これが後のビッグバン理論に続くわけだけども、科学者たちはその後の宇宙の未来に興味を移した。というのも、宇宙が広がっているからと言って、それが一生続くかどうかはわからない。大きく分けると、宇宙の広がり方には２種類の可能性が存在するのだ。

ひとつは、加速しながら宇宙が広がっている可能性。

もうひとつは、減速しながら宇宙が広がっている可能性である。

加速と減速で何が違うんだと思われるかもしれないが、よく考えれば全然違う未来が待っているのだ。

加速して宇宙が広がっている場合は、イメージしやすいと思うが、そのまま時空間がどんどん広がっていくことだろう。

しかし、もし減速しながら宇宙が広がっている場合、宇宙は最終的に縮んでいく運命にあるのだ。確かに、今は宇宙の始まりのビッグバンなどにより時空間は広がっているかもしれないが、その広がりのスピードは減速しているので、ある一定まで広がった後は縮小に転じるのである。

当時の科学者の間では、後者の減速しながら広がっている宇宙が支持されていた。なぜなら何もない空間（宇宙）には少なくとも物質が存在しているので、それらの持つ引力によってお互いを引き付け合い、縮小していくと考えられていたからだ。普段地球から受ける引力が強すぎるため感じられないが、質量を持つ物体同士には引き合う力（引力）が存在している。

見えない質量が存在する可能性

さらに１９３３年に、スイスの物理学者ツヴィッキーが、自分たちが目に見えるもの以外に質量をもつものが存在する可能性を示唆した。

彼は銀河の回転速度を調べていた。銀河の中心からの距離とそこの質量によって回転速度が決まる。

その方程式は、回転運動しているので、遠心力($F_c$)と引力($F_g$)が釣り合っている式から導かれる。回転速度を$v$、銀河の中心からの距離を$r$、銀河の質量を$M(r)$で表す。銀河の質量$M$に$(r)$がついているのは、距離$r$によって質量が変わっていますよ、という意味だ。

$$F_c=\frac{m v^2}{r}$$

$$F_g=\frac{G M(r) m}{r^2}$$

それらが釣り合っているので

$$F_c=F_g$$

とすると

$$v=\frac{M(r) G}{r}$$

これが銀河の回転速度が、距離$r$とその質量$M(r)$によって決まるという式だ。

銀河からの距離が近ければ近いほど分母にある$r$が小さくなるので、最終的な銀河の回転速度$v$は大きくなりそうだ。逆に銀河の中心から遠いところの回転速度は、分母の$r$の値が大きくなるので、銀河中心の回転速度に比べて小さくなりそうだ。

ちなみに、銀河の重さというのは、写真を撮って星の数を数えてやることで大体の質量が計算できる。

そうやって数え上げた星から算出された銀河の回転速度は下の図の点線Aのようであるべきだとツヴィッキーは考えた。

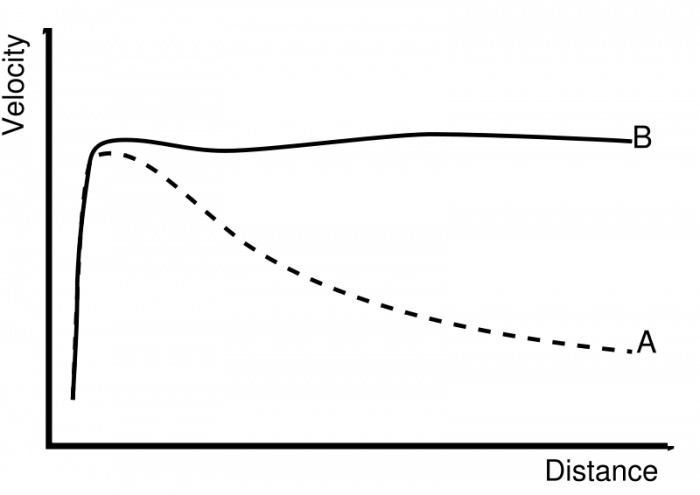
外側に行けば行くほど回転速度が小さくなっているのがわかるだろう。

しかし、実際の銀河の回転速度を計測してみると実線Bのようであり、外側に行ってもあまり中心と回転速度が変わらないのがわかる。これは計算すると、見かけによる質量の４００倍もの質量が存在していないと説明がつかないのだった。

この目に見えない質量の存在をダークマターと呼ぶようになったのだ。

このこともあり、宇宙の広がり方は減速している説がさらに有力になった。目に見えている星だけじゃなく、謎の質量がもっと存在しているのだから、宇宙の縮み方はもっと速いだろうと考えたのだった。

しかしこれも実は間違いだったのだ。宇宙は加速しながら膨張しているというのが今の主流だ。

奇しくも、アインシュタインの定常的な宇宙が間違いであったことを証明したハッブルの名を冠した衛星宇宙望遠鏡が宇宙の加速膨張を証明した。目に見える星のみならず、ダークマターの引力の効果を打ち消すどころか、宇宙空間を加速しながら膨張させる何かが存在しているのだ。我々はそれをダークエネルギーを呼ぶことにしている。

ダークエネルギーの話はまた別の機会に話そう。