
少し前に美人すぎる女性物理学者という記事を書いた。
その中に物理学者ではなく、ひとり数学者を紛れ込ませた。クリオ・クレスウェルというオーストラリアの数学者だ。彼女は「完璧なパートナーを見つけるためには12人と付き合った人から選びなさい」 という主張した『Mathematics and sex(数学と性)』という有名な本の著者でもある。

彼女のTEDを聴いていると、自分の理論だけでなく数学が社会でどのように使われているかといくつか紹介していた。
結婚生活に関する数式、抗生物質の効用に関する数式…などいろいろ紹介してくれていたのだが、彼女のお気に入りの数式としてひとつ紹介されたのが
「完ぺきなチョコレートを作る数式」
であった。
数式はこんな感じ
$$\rho_l C_p \frac{\partial T}{\partial t}=\textit k_{eff} \Delta T -\frac{3 c_0 \textit k}{R_0 ^2 \rho_s}\bigg(\bigg(1+\frac{1}{f}\bigg)(T-T_m)\bigg)\sqrt[3]{\frac{c}{c_0}}$$
$$\frac{dc}{dt}=-\frac{3 c_0 \textit k}{R_0 ^2 L \rho_s}\bigg(\bigg(1+\frac{1}{f}\bigg)(T-T_m)\bigg)\sqrt[3]{\frac{c}{c_0}} $$

ここでいう完ぺきなチョコレートというのは、部屋の常温では溶けずに、口の中の温度でうまく溶けるチョコレートのことだ。
チョコレートの原材料というのは、カカオとココアバター(カカオからとれる油)に砂糖などを組み合わさってできている。
もちろん、それらを配合する割合も「完璧なチョコレート」を作る上で大切なのだが、この論文によるとチョコレートに核となるココアバターの粒を入れるタイミングだったり、周りの温度が重要な要素となっているようだ。
実験方法としては、様々な溶かしたチョコレート自体の温度や周りの温度の組み合わせの中で、ベストなココアバターを入れるタイミングを調べている。
細かい実験方法は端折るが
もう一度方程式を見てみよう
$$\rho_l C_p \frac{\partial T}{\partial t}=\textit k_{eff} \Delta T -\frac{3 c_0 \textit k}{R_0 ^2 \rho_s}\bigg(\bigg(1+\frac{1}{f}\bigg)(T-T_m)\bigg)\sqrt[3]{\frac{c}{c_0}}$$
左辺にある、\(\rho_l\)は液体チョコレートの単位質量、\(C_p\)は熱容量、\(T\)は温度、\(t\)はもちろん時間を表している。\(T\)と\(t\)が偏微分の形式で書かれているが、それは時間と共に温度が変わるからだ。しかし、これは熱力学で学ぶ
$$Q=mc\Delta T$$
によく似ている。というか時間と共に変わる比熱の式そのものだ。温度が変化すれば熱量は変化する当たり前のことだ。
問題は右辺である。
\(k_{eff}\ (effective\ thermal\ conductivity)\)はどれぐらい熱が通りやすいかという定数なので、チョコレートによって違うかもしれないが、決まった数字が入る。それから\(\Delta T\)があるが、温度の変化量を示している。
右辺の2項目は、(かっこ)の前に\(c_0\)やら\(k\)やら\(R_0\)やら\(\rho_s\)やらあるが、全部結局はほぼ初期条件の定数である。(かっこ)の後ろにある\(\sqrt[3]{\frac{c}{c_0}}\)の中の\(c\)は2つ目の式で導かれるものだ。
その2つ目の式をもう一度見てみよう
$$\frac{dc}{dt}=-\frac{3 c_0 \textit k}{R_0 ^2 L \rho_s}\bigg(\bigg(1+\frac{1}{f}\bigg)(T-T_m)\bigg)\sqrt[3]{\frac{c}{c_0}} $$
左辺はココアバターの密度の時間変化を表していて、右辺はひとつ目の式の右側とほとんど同じだ。分母に\(L\)があるけど、これもチョコレートの潜熱なのでやはり定数である。
ということは
これらの式で重要になってくるのは、(かっこ)の中のようだ。
\(f\)は\(\Delta R/R\)というココアバターの粒の層の厚さとその粒の半径との割合だ。これは本来時間と共に変化する割合だが、実験によると、\(f=1.3\)という数値を使えば現実のチョコレートの温度変化と一致するようだ。
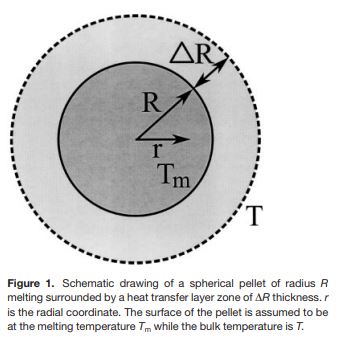
(かっこ)の中には\(T\)と粒が溶ける温度\(T_m\)があるが、特に\(T\)というのは初期の温度や周りの温度に影響されるので、いかに温度の初期値が重要であるかがわかる。
実験結果としては
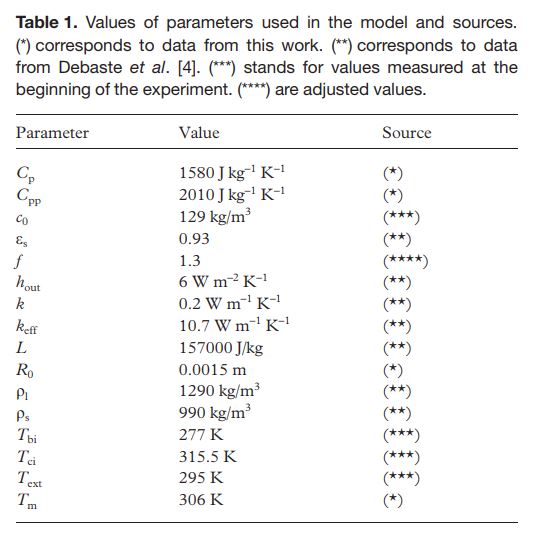
星が3つあるのは「完璧なチョコレート」を作るのに必要なデータ(特に温度)と最終的にこの数式モデルを現実に合わせるために調整して得られた星4つの\(f=1.3\)という値。
自分も細かいところはわかっていない。
でもわかってもらいたいのは、チョコレートにも数式が使われているという事実だ。
参考 『Modeling temperature in chocolate mass to predict tempering quality』





コメント