固有値と固有ベクトルはどう使う（応用）

固有値や固有ベクトルの利用法
1. 利用例１：動的システム
利用法２：統計学（主成分分析）
利用法３：シュレディンガー方程式

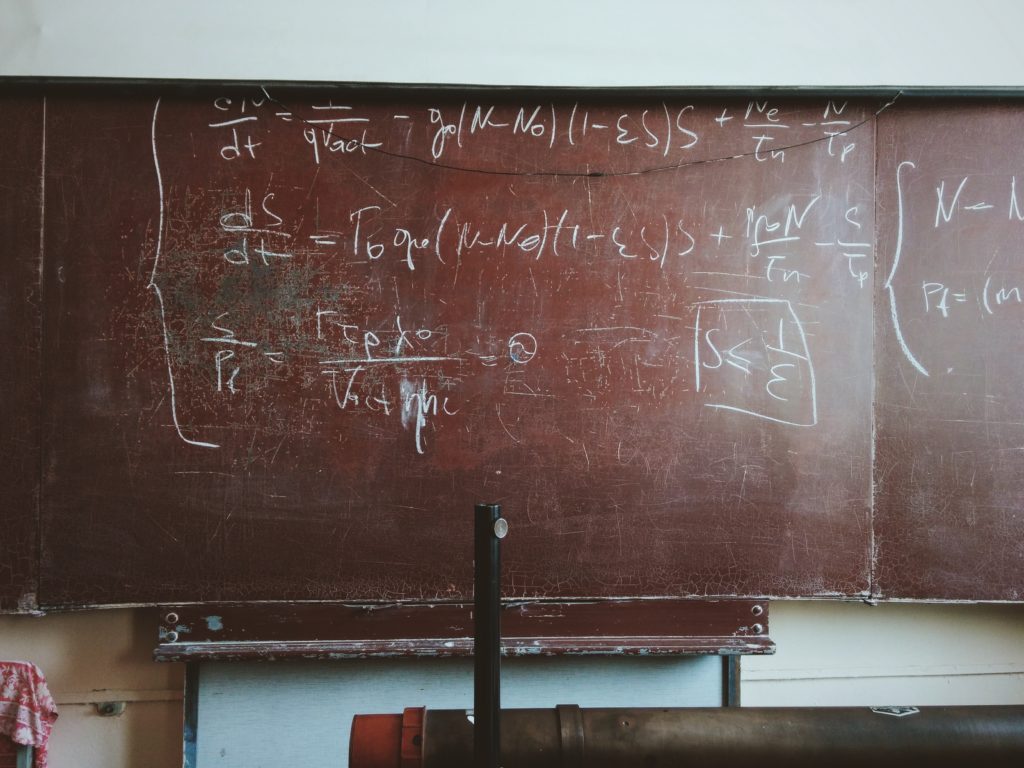
固有値や固有ベクトルの利用法

数学や物理を学んでいると線形代数学という学問を勉強する。　　　　　　　　　　　

連立方程式を解くテクニックとして始まったものらしいが、意外にも奥が深く、ひとつの学問として昇華したようだ。

たくさんの連立方程式を簡単に解くことのできるいくつかのテクニックには、「おおすごい！」と感動したものだけど、途中からどうも抽象性が増して、勉強していてもこれがどのように役立つのかわからない、という感じで進めていた。この気持ちは僕だけではないと信じたい。

その線形代数の中に、固有値と固有ベクトルというトピックがある。

（ちなみに英語では$Eigenvalue と Eigenvector$といい、僕は英語で最初に学んだもんだから、日本語訳の固有値っていう言葉を聞いても、$Eigenvalue$のことだとは思わなかった。英語訳かっこよくない？）

$A$：行列、$\vec{\ x\ }$：ベクトル、$λ$：スカラー（数）を使って、

$$A\vec{\ x\ }=λ \vec{\ x\ }$$

と書く。普通、あるベクトルに行列をかけ合わせると、ベクトルの向きや大きさが変わるのだけども、中にはそのベクトルの向きが変わらず、大きさだけが変わる組み合わせがある。それが固有値と固有ベクトルの組み合わせだ。

たとえば、$\begin{align*}A \ =\ \left(\begin{array}{cc}2 & 3 \\2 & 1 \end{array}\right)\end{align*}$ という行列と$\vec{x}=\left(\begin{array}{c}1\\3 \end{array}\right)$というベクトルをかけ合わせてみよう。

すると

$$\left(\begin{array}{c}2 & 3 \\2 & 1\end{array}\right)\left(\begin{array}{c}1\\3 \end{array}\right)=\left(\begin{array}{c}11\\5 \end{array}\right)$$

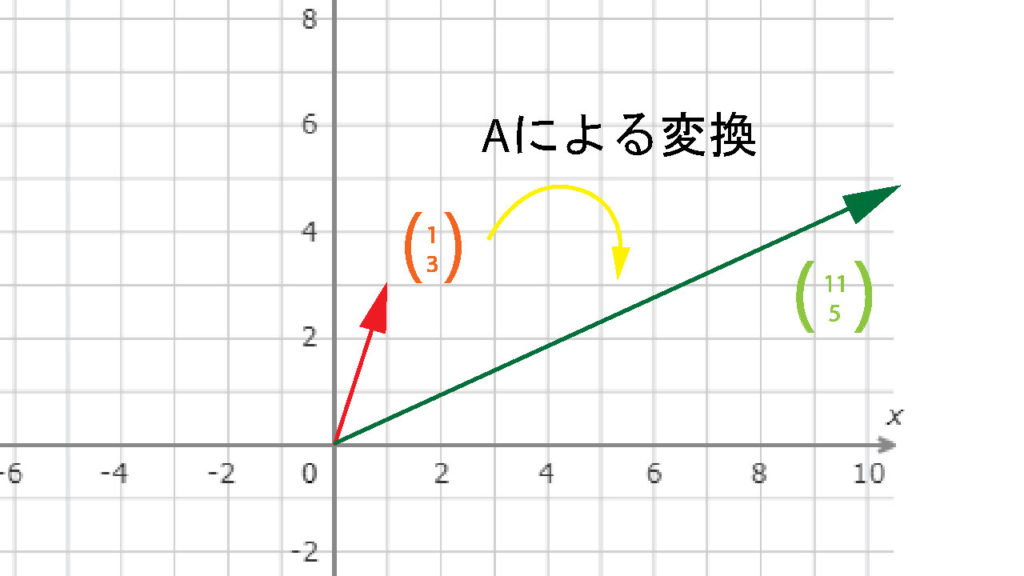
となり、もともとのベクトルの大きさだけでなく、方向も変わってしまったことになる。そういった意味では、行列をかけ合わせるというのは、ベクトルを座標上で変換させる性質を持つと言える。

ところが、行列とベクトルの組み合わせによっては、ベクトルの大きさが変わるだけで、方向が変化しないものもある。

たとえば

$$\left(\begin{array}{c}2 & 3 \\2 & 1\end{array}\right)\left(\begin{array}{c}3\\2 \end{array}\right)=\left(\begin{array}{c}12\\8 \end{array}\right)
=4×\left(\begin{array}{c}3\\2 \end{array}\right) $$

となって、もともとの$\vec{x}$を４倍したベクトルになった。このときの
$\vec{x}$ を固有ベクトル、４というスカラー（数値）を固有値と呼んでいる。

概念自体は難しいものではないし、計算自体も難しいわけでもない。

詳しい解説は他の教科書や解説サイトに任せることにするけども、この固有値や固有ベクトルをどのように使ったり、応用するのかを書いてあるものは少ない。

ここではそれらを実際にどのように使うのかを調べて記しておきたい。

さまざまな分野で使われているようだけど、主に使われているのは

動的システム

統計学（主成分分析）

量子力学（シュレディンガー方程式）

などだ

利用例１：動的システム

ここでの動的システムは生物学を意識して使っている。あるエリアにいる２種類の生物の数が、一定時間後にどう変化するのか考えるのだ。そこで、こういう式を用意したい。

$$\vec{x}_{k+1}=A\vec{x}_{k}$$

$x$の上に矢印が付いているが、それはベクトルを表している。この $\vec{x}$には２種類の生物の数が含まれている。ただの２種類の生物の数なのにベクトルとして表現するのはいかがなものかと思うかもしれないけれど、２つの数字を同時に扱うという点ではベクトルでの表現は適切である。この式は、$k$時点から少し経過したときの生物の個体数の増減を表したりする。$A$という係数をかけ合わせることによって一定時間後のそれぞれの生物の数が決まるのだ。

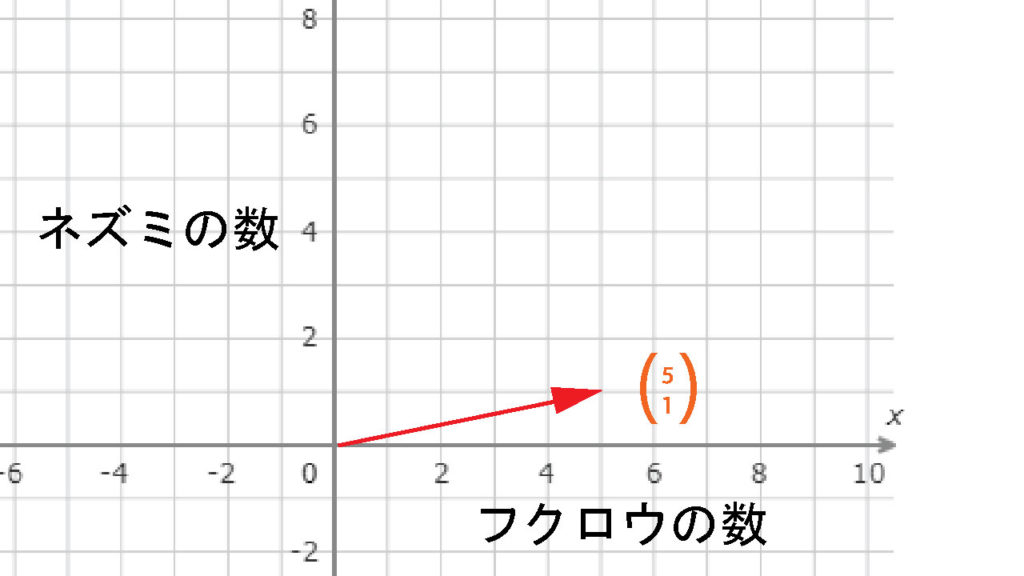
例えば、森の中にいるフクロウ$O$とその獲物であるネズミ$R$ の数の増減などであるが

$$\vec{x}_{k}=\left(\begin{array}{c}O_{k}\\R_{k} \end{array}\right)$$

と$O$と$R$という２つの数で表す。

２次元の座標上では、横向きをフクロウの数（$O$）を、縦の軸はネズミの数（$R$）を表している。

たとえば、ある時点でのフクロウの数（$O$）が５、ネズミの数（$R$）が１だとすると

次に左辺の$\vec{x}_{k+1}$を考えていきたい。

ひとつは $O_{k+1} $、$k+1$と書いてあるが、これはある$k$という時点から一定時間後（実際の計測は１か月後）のフクロウの数を式で表したものである。

$$O_{k+1}=0.5O_{k}+0.4R_{k}$$

つまり来月のフクロウの数は、現時点でのフクロウの数とネズミの数に依存するという式である。フクロウ的にはそのエリアで同じフクロウが多ければ、獲物であるネズミを取り合うために数を減らすかもしれないし、そもそもそのネズミの数が多いか少ないかによって状況が変わる、というような感じだ。

$ｋ$から１ヵ月後のフクロウの数は、$k$時点のフクロウの数の半分に、$k$時点のネズミの数の４０％を足した数になるというものだ。（実際はネズミの数はこの数字の１０００倍だが、話を簡単にするために１０００分の１の数を扱っている。）

次はネズミの数の式

$$R_{k+1}=-0.104O_{k}+1.1R_{k}$$

これは、$k$時点から１か月後のネズミの数である。右辺のはじめの項にはマイナスが付いているのだけど、$k$時点のフクロウの数に比例して捕食される可能性増加のために数が減ると思われるので納得できるだろう。最後の項は、$k$時点のネズミの数の１０％増えるという意味だ。

もちろん、初期値（ここでは初めのフクロウとネズミの数）によって、毎回の増減の割合が変わってくるのだけど、どうにかこのシステムをもっと一般化できないか。

そこで使えるのが、固有値と固有ベクトルだ。

まずやるべきことは、この２つの式の係数を行列$A$と見立て、$k$時点でのフクロウの数$O_{k}$とネズミの数を$R_{k}$いうベクトルの要素として扱って、システムの動向を調べることだ。

係数の部分はひとつにまとめられ、

$$\begin{align*}A \ =\ \left(\begin{array}{cc}0.5 & 0.4 \\-0.104 & 1.1 \end{array}\right)\end{align*}$$

フクロウとネズミの数も

$$\vec{x}_{k}=\left(\begin{array}{c}O_{k}\\R_{k} \end{array}\right)$$

こう書ける。もう一度固有値と固有ベクトルの式を見てみよう。

$$A\vec{\ x\ }=λ \vec{\ x\ }$$

$$\begin{align*} \left(\begin{array}{cc}0.5 & 0.4 \\-0.104 & 1.1 \end{array}\right)\end{align*}\left(\begin{array}{c}O_{k}\\R_{k} \end{array}\right) =λ\left(\begin{array}{c}O_{k}\\R_{k} \end{array}\right) $$

確かに、これらが固有値と固有ベクトルの組み合わせを見つければ、時期に関係なくフクロウとネズミの数がどのように増えたり減ったりするのかがわかるだろう。

$$det(A-λE)=0$$

この固有方程式を解いてやれば、固有値$λ$を求めてやることができる。この式での$λ$の解は２つあり、計算過程は省くが、$λ_{1}＝1.02$、$λ_{2}＝0.58$となる。ちなみに、導き出された$λ$の中で数値が大きい方が、そのシステムの中で優勢になることが知られている。このことは後でわかる。

そこからそれぞれの$λ$を使って連立方程式を解くと、それぞれの$λ$に対応した固有ベクトルが計算される。結果だけを示すが$\vec{v}_{1}=\left(\begin{array}{c}10\\13 \end{array}\right)$、$\vec{v}_{2}=\left(\begin{array}{c}5\\1 \end{array}\right)$である。

ここで２つ固有値と固有ベクトルの組み合わせの式ができた。

$$\begin{align*}A\vec{v}_{1} \ =\ \lambda_{1} \vec{v}_{1}\end{align*}$$

$$\left(\begin{array}{c}0.5 & 0.4 \\-1.04 & 1.1\end{array}\right)\left(\begin{array}{c}10\\13 \end{array}\right)=(
1.02)\left(\begin{array}{c}10\\13 \end{array}\right)$$

$$\begin{align*}A\vec{v}_{2} \ =\ \lambda_{2} \vec{v}_{2}\end{align*}$$

$$\left(\begin{array}{c}0.5 & 0.4 \\-1.04 & 1.1\end{array}\right)\left(\begin{array}{c}5\\1 \end{array}\right)=(
0.58)\left(\begin{array}{c}5\\1 \end{array}\right)$$

である。まだ完全にこのシステムの一般的な式とは言えないけども、ある時点$k$でフクロウとネズミの数が１０対１３（$\vec{v}_{1}$）という割合であるならば、次の１か月後には１．０２（$λ_{1}$）倍の数になっていて、もしフクロウとネズミの数が５対１（$\vec{v}_{2}$）という割合ならば、１か月後には０．５８（$λ_{2}$）倍の数になっているということである。

しかしそんな都合よくその割合になることなんてほとんどない。もっと簡潔な式にならないだろうか。ここからは固有値と固有ベクトルの範囲から外れるかもしれないが、方法はある。

まず初期値（一番最初のフクロウとネズミの数）を

$$\vec{x}_{0}=c_{1}\vec{v}_{1}+c_{2}\vec{v}_{2}$$

と置くのである。$c$はスカラー（数）で、これを固有ベクトルの前に置くことでさまざまな初期の個体数に対応できるようにしてある。これまでに求めた固有ベクトルの値は変わらない。

１ヵ月後の式を$x_{1}$と置いて

$$\vec{x}_{1}=A\vec{x}_{0}=c_{1}A\vec{v}_{1}+c_{2}A\vec{v}_{2}$$

と表すことができる。係数の値はそのままだから行列$A$の値はいつでも変わらない。固有値と固有ベクトルの関係から、$A$の代わりに$λ$を掛け合わせることができる。そうするとこんな感じの式になる。

$$\vec{x}_{1}=c_{1}λ_{1}\vec{v}_{1}+c_{2}λ_{2}\vec{v}_{2}$$

$$\vec{x}_{1+1}=\vec{x}_{2}=A\vec{x}_{1}=c_{1}λ^{2}_{1}\vec{v}_{1}+c_{2}λ^{2}_{2}\vec{v}_{2}$$

$$\vec{x}_{2+1}=\vec{x}_{3}=A^{2}\vec{x}_{1}=c_{1}λ^{3}_{1}\vec{v}_{1}+c_{2}λ^{3}_{2}\vec{v}_{2}$$

式の中から$A$が消えた。それから、数字の代わりに$k$を代入してみよう。$k$という数だけ$λ$をかけ合わせるのだから、こんなかたちになる。

$$\vec{x}_{k}=c_{1}λ^{k}_{1}\vec{v}_{1}+c_{2}λ^{k}_{2}\vec{v}_{2}$$

それぞれの固有ベクトル$\vec{v} $も、それらに対する固有値$λ$も変わらない。代入するとこうなる。

$$\vec{x}_{k}=c_{1}(1.02)^{k}\left(\begin{array}{c}10\\13 \end{array}\right)+c_{2}(0.58)^{k}\left(\begin{array}{c}5\\1 \end{array}\right)$$

長い期間経つとどうなるか考えるために、ここで$k$を無限大にまで大きくしてやる。

すると$k$を指数に持つ$0.58^{k}$という値は限りなく０に近づくので、２番目の項を無視してやることができ,

$$\vec{x}_{k}\approx c_{1}(1.02)^{k}\left(\begin{array}{c}10\\13 \end{array}\right)$$

となった。最後に$\vec{x}_{k+1}$を考えると、

$$\vec{x}_{k+1}\approx c_{1}(1.02)^{k+1}\left(\begin{array}{c}10\\13 \end{array}\right)=(1.02)c_{1}(1.02)^{k}\left(\begin{array}{c}10\\13 \end{array}\right)\approx 1.02\vec{x}_{k}$$

$c_{1}(1.02)^{k}\left(\begin{array}{c}10\\13 \end{array}\right)$の部分は$\vec{x}_{k}$と同じなので、最終的に$1.02\vec{x}_{k}$となった。

これからわかったのは、最終的にフクロウとネズミの割合は１０対１３に落ち着き、その数が毎月２％づつ増加するというものである。固有値を求めたとき、その数値の大きい方が優勢になるということを言ったのは、この結果のためである。

固有値と固有ベクトルの概念を使って生物学の動的システムを一般化することができた。これが固有値と固有ベクトルの応用法のひとつである。