今回は大阪で集まって勉強しました。

学生さんは学校が始まり、休日はなかなか予定が合わないので、平日の夜に勉強会を開催しました。
前回、集まったときは時間短かったですけれど、今回は3時間がっつり時間使って勉強しました。なんとこの部屋、3時間使って550円なんですね。安い!助かる!
今回は、学生のO君にリードしてもらいました。これまでは、僕が適当に知っていることをゆっくり話す、というスタイルだったのですが、学習スピードの速いO君に任せることにしました。
すると、スゴいんです。
確かに彼の説明は、頭がいい人の特有の細切れの解説で、頭の回転の遅い僕なんかはついていくのが大変だったんですが、知識の量や計算能力の高さは飛びぬけていて、とっても勉強になりました。
ホント、本物の学生と付け焼刃の知識しか持ち合わせていない僕との力の差を痛感しました。理解していたつもりではあったけど、こんな状態で大学院にも行きたいと考えていた自分が恥ずかしくなるぐらいです。
しかし、そもそもこの宇宙物理勉強会は「大学とか行っていなくても物理を勉強しよう」というのが趣旨でした。なので、悔しいとか恥ずかしいという感情よりも、力のある学生と一緒に勉強できる環境があってよかった、という気持ちです。(僕も大人になったんでしょうか笑)
現在は、相対性理論を共通のトピックとして扱っています。\(E=mc^{2}\)を導出するところまでやったので、現在は電磁気学のマクスウェル方程式をひとつにまとめるところをやっているんですが、今回良かったのは、途中でO君が高校生時代に学んだ数学の中でおもしろかったと思うものを紹介してくれました。
それは等差数列の和の公式とかべき乗和の公式と呼ばれているみたいです。
\(S_1 = \sum_{n=1}^l n = \frac{l(l+1)}{2}\)
\(S_2 = \sum_{n=1}^l n^{2} = \frac{l(l+1)(2n+1)}{6}\)
その後、導出はしていませんが
\(S_3 =\sum_{n=1}^l n^{3} = (\frac{l(l+1)}{2})^{2}\)
の紹介もし、1番最初に紹介した\(S_1\)の2乗が\(S_3\)になることに感動していました。
つまり
\((1+2+3+…+l)^{2} = 1^{3}+2^{3}+3^{3}+…+l^{3}\)
ということになります。1乗の和を2乗すると3乗の和になるのは何とも不思議な感覚です。
この導出が相対性理論に必要という訳ではありませんが、シグマ\(\Sigma\)がときどき出てくるので、復習がてらこの話をしてくれました。
脱線の話もおもしろいのはとてもいいことです。
その後は、4つのマクスウェル方程式を観賞したり、最終目標である標準理論や超ひも理論の方程式をホワイトボードに書き写したものを眺めて時間を過ごしました。
映画とか絵を一緒に観賞するのではなく、方程式を一緒に眺めて時間を過ごすというのはなかなかオシャレでしょ?
こういうことをしたのも、実はもうひとりの参加者であるTさんのおかげでもあるんです。
Tさんは数学や物理は素人なんですが、どうやら東洋医学に関する知識は相当なもので、さまざまな事柄に関して、その観点から「整っている」か「整っていない」の判断ができるそうで、いろんな方程式を見比べてもらったのです。
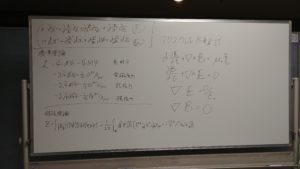
合ってるかはわかりません。意味も分からないまま書き写しただけなので(笑)
次は、マクスウェル方程式を相対性理論でひとつにします。
大阪に住んでいる方で興味のある方はこちらで連絡してください。
これまでの勉強会↓




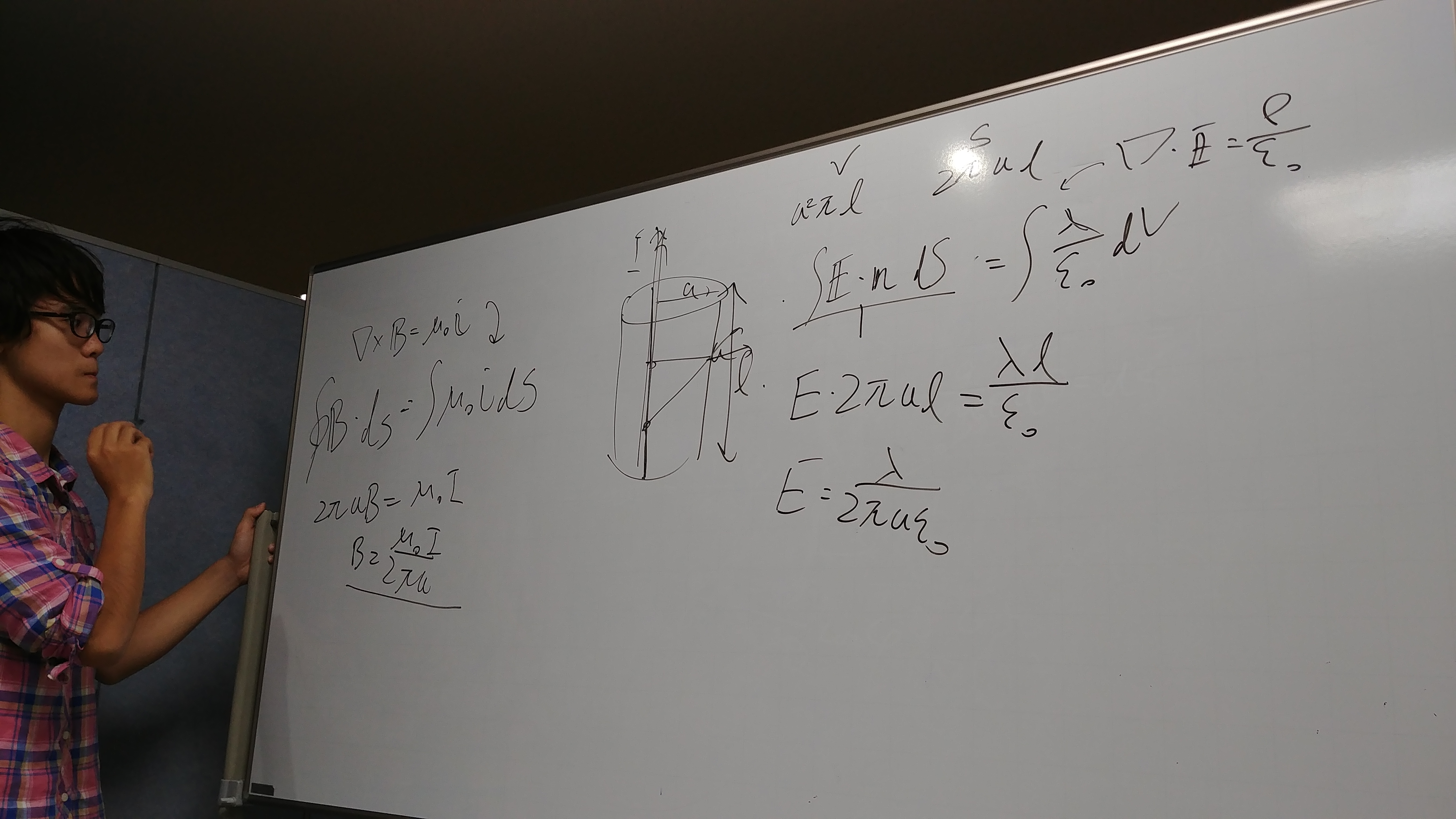
コメント