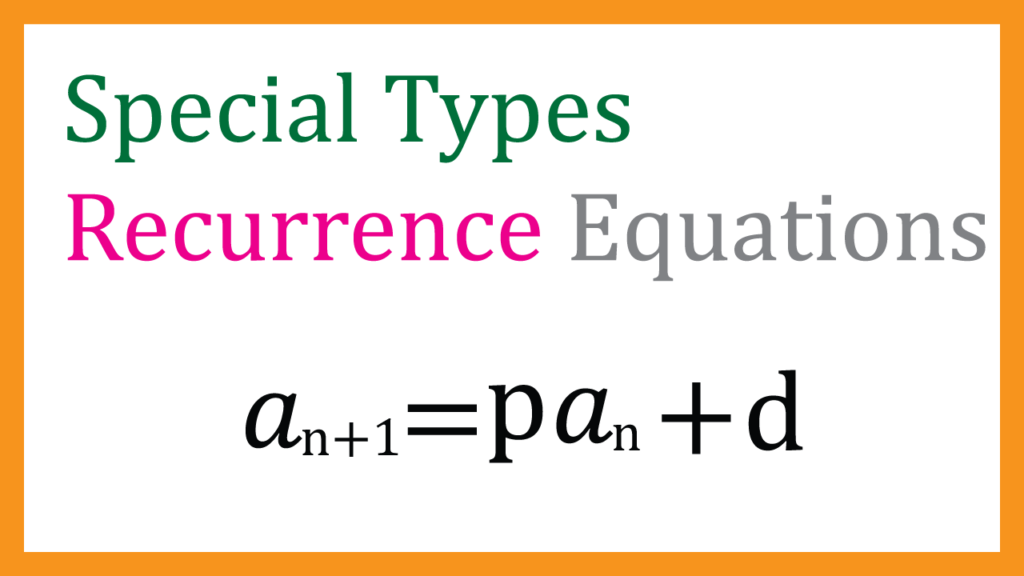
Special types of Recurrence Equations
Seems this is one of the most difficult topics in EJU math
If you want to know 3 basic recurrence equations,
please read above first
$$Type:\ \ a_{n+1}=p a_n + q $$
Method: Use characteristic equation to transform the original equation into a geometric progression
Example
$$a_1=3,\ a_{n+1}=2a_n – 1$$
Use Charasteric Equation (put \(\alpha\) into \(a_n\) and \(a_{n+1}\))
$$\alpha=2 \alpha -1$$
$$\alpha = 1$$
Subtract the characteristic equation from the original one
$$
\begin{array}{rcccccc}
& a_{n+1} &= & 2a_n – 1
\\ -)& \alpha &= &2\alpha – 1
\\\hline & a_{n+1} -\alpha &= & 2(a_n – \alpha)
\end{array}
$$
Since \(\alpha = 1\)
$$a_{n+1}-1 = 2(a_n -1)$$
If you set \(b_{n+1} = a_{n+1}-1 \) and \(b_n= a_n-1\)
$$b_{n+1}=2 b_n$$
This is the recurrence equation of the geometric progression
Use the formula of geometric progression
$$a_n=a_1 r^{n-1}$$
$$b_n=b_1 2^{n-1}$$
$$a_n-1=2^{n-1}(a_1-1)$$
Arrange it
$$a_n=2^n+1$$
$$Type:\ \ a_{n+1}=\frac{a_n}{p a_n +q} $$
When you see
$$a_{n+1}=\frac{a_n}{p a_n +q}$$
It’s called Fractional type
Method: We need to arrange and change it to \(a_{n+1}=p a_n + q \ Type\)
Example
$$a_1=3,\ a_{n+1}=\frac{2 a_n}{3 a_{n+1}}$$
Get reciprocal fraction of it
Also make sure if \(a_n ≠0\)
$$(a_{n+1})^{-1}=\bigg(\frac{2 a_n}{3 a_{n+1}}\bigg)^{-1} $$
$$\frac{1}{a_{n+1} }=\frac{3a_{n+1}}{2a_n}$$
$$=\frac{3}{2}+\frac{1}{2} \frac{1}{a_n}$$
If you set \(b_{n+1}=\frac{1}{a_{n+1}},\ b_n=\frac{1}{a_n}\) as a new sequence
$$b_{n+1}=\frac{1}{2}b_n+\frac{3}{2}$$
Remember it is
$$Type:\ \ a_{n+1}=p a_n + q$$
Solve the characteristic equation
$$\alpha = \frac{1}{2}\alpha + \frac{3}{2}$$
$$\alpha=3$$
$$b_{n+1}- \alpha = p(b_n- \alpha)$$
$$\frac{1}{a_{n+1}}-3= \frac{1}{2}\bigg(\frac{1}{a_n}-3\bigg)$$
This is a geometric progression
If you set \(c_{n+1}=
\frac{1}{a_{n+1}}-3 \ c_n=
\frac{1}{a_n}-3 \)
$$c_{n+1}=\frac{1}{2}c_n$$
Use the formula of a geometric progression, then
$$c_n=c_1\bigg(\frac{1}{2}\bigg)^{n-1}$$
So
$$\frac{1}{a_n}-3=\bigg(\frac{1}{2}\bigg)^{n-1} \bigg(\frac{1}{a_1}-3\bigg)$$
Since \(a_1=3\) is given
$$\frac{1}{a_n}-3 =\bigg(\frac{1}{2}\bigg)^{n-1} \bigg(\frac{1}{3}-3\bigg) $$
If you solve for \(a_n\)
$$a_n=\frac{3・2^{n-4}}{-1+9・2^{n-4}}$$
$$Type:\ \ (a_n)^m,\ \ (a_{n+1})^n$$
Let’s call this exponent type
Method: Use logarithm to transform it into \(a_{n+1}=pa_n+q\), then deal with a geometric progression
Example
$$a_1=4,\ \ a_{n+1}=2a_{n}^2$$
We need to use logarithm
Our goal is to get the form \(a_{n+1}=pa_n+q\) by arranging the original equation
Let’s take log for both sides of \(a_{n+1}=2a_{n}^2 \)
$$\log_{2}a_{n+1}=\log_{2}2a_n^2$$
$$=1+2\log_2 a_n$$
if we set \(b_n=\log_2 a_n\)
$$b_{n+1}=2b_n +1$$
Solve the characteristic equation
$$\alpha = 2\alpha +1$$
$$\alpha = -1$$
Set \(b_{n+1}+1=2(b_n+1)\)
If you consider that \(c_{n+1}=b_{n+1}+1,\ \ c_n=b_n+1\)
$$c_{n+1}=2 c_n$$
is a geometric progression
Use the formula for geometric progression
$$c_n=c_1 ・2^{n-1}$$
Since
$$c_{1}=b_1+1$$
$$=\log_2 a_1+1$$
$$=\log_2 4 +1$$
$$=3$$
Hence
$$c_n=c_1 ・2^{n-1}$$
$$b_n+1=3・2^{n-1}$$
$$b_n=3・2^{n-1}-1$$
Therefore
$$\log_2 a_n =3・2^{n-1}-1 $$
$$a_n=2^{3・2^{n-1}-1}$$
$$Type:\ \ a_{n+1}=pa_n + r^n$$
Method: Divide by \(r^{n+1}\) for both sides, and convert it to \(Type:\ \ a_{n+1}=pa_n + q\)
Example
$$a_1=3,\ \ a_{n+1}=2a_n -3^n$$
We do not want to have \(n\) on the shoulder of \(3\)
So, let’s divide by \(3^{n+1}\)
$$\frac{a_{n+1}}{3^{n+1}}=\frac{2a_n}{3^{n+1}}-\frac{3^n}{3^{n+1}}$$
$$\frac{a_{n+1}}{r^{n+1}}=\frac{2}{3}・\frac{a_n}{3^n}-\frac{1}{3}$$
If you consider that \(\frac{a_{n+1}}{3^{n+1}}\) & \(\frac{a_n}{3^n}\) as a new sequence, then we can have a characteristic equation
$$\alpha = \frac{2}{3}\ \alpha \ – \frac{1}{3}$$
If we solve for \(\alpha\),
$$\alpha = -1$$
Use \(a_{n+1}-\alpha=p(a_n-\alpha) \)
$$\frac{a_{n+1}}{3^{n+1}}+1=\frac{2}{3}\bigg(\frac{a_n}{3^n}+1\bigg)$$
If we set \(b_n = \frac{a_n}{3^n}+1\),
$$b_{n+1}=\frac{2}{3}b_n$$
Since this is a geometric progression,
$$b_n=b_1 r^{n-1}$$
Since \(b_1=\frac{a_1}{3}+1=2\)
$$\frac{a_{n}}{3^{n}}+1=2\bigg(\frac{2}{3}\bigg)^{n-1}$$
$$\frac{a_{n}}{3^{n}}+1=\bigg(\frac{2}{3}\bigg)^{n-1}$$
$$a_n=3^n\bigg(\bigg(\frac{2}{3}\bigg)^{n-1}-1\bigg)$$
End of the day
$$a_n=2^n・3^{-n+2} – 3$$
$$Type: \ \ a_{n+2}=p a_{n+1}+ q a_n$$
If you see \(a_{n+2}\) in the relation, we need to use ANOTHER type pf characteristic equation.
Example
$$a_1=2,\ \ a_2=3,\ \ a_{n+2}=2a_{n+1}+3a_n$$
First of all, we have to set the followings to make a characteristic equation with \(t\)
$$t^2=a_{n+2},\ \ t=a_{n+1}, \ \ 1= a_n$$
Now we have
$$t^2=2t+3$$
This is new type of characteristic equation for 3 terms recurrence equation.
If we solve for \(t\),
$$t^2-2t-3=0$$
$$t=-1,\ \ 3$$
Set
$$\alpha=-1, \ \ \beta=3$$
*it does not matter which letter you use for \(-1\).
Transform the original equation to
$$a_{n+2}-\alpha a_{n+1}= \beta (a_{n+1}-\alpha a_n)$$
Then we get
$$a_{n+2}+a_{n+1}=3(a_{n+1}+a_n)$$
If you set
$$b_{n+1}=a_{n+2}+a_{n+1},\ \ b_n=a_{n+1}+a_n $$
we can have
$$b_{n+1}=3 b_n$$
Since this is a geometric progression,
$$b_n=b_1 3^{n-1}$$
$$a_{n+1}+a_n=3^{n-1}(a_{1+1}+a_1)$$
$$a_{n+1}+a_n=3^{n-1} ・5$$
$$a_{n+1}=-a_n+5・3^{n-1}$$
Remember that it is Type \(a_{n+1}=pa_n + r^n\)
Therefore we should divide by \(r^{n+1}\) for both sides to transform it into Type\(a_{n+1}=p a_n + q\)
$$\frac{a_{n+1}}{3^{n+1}}= -\frac{a_n}{3^{n+1}}+\frac{5・3^{n-1}}{3^{n+1}}$$
$$\frac{a_{n+1}}{3^{n+1}}= -\frac{1}{3}・\frac{a_n}{3^{n}}+\frac{5}{9} $$
Solve the characteristic equation
$$\alpha=-\frac{1}{3}\alpha+\frac{5}{9}$$
$$\alpha=\frac{5}{12}$$
Set \(a_{n+1}-\alpha=p(a_n-\alpha) \)
$$\frac{a_{n+1}}{3^{n+1}}-\frac{5}{12}=-\frac{1}{3}\bigg(\frac{a_n}{3^n}-\frac{5}{12}\bigg)$$
$$b_{n+1}=r b_n$$
$$b_{n+1}=-\frac{1}{3} b_n$$
$$b_n=b_1 r^{n-1}$$
$$\frac{a_{n}}{3^{n}}-\frac{5}{12}=-\bigg(\frac{1}{3}\bigg)^{n-1}\bigg(\frac{2}{3^n}-\frac{5}{12}\bigg)$$
Eventually
$$a_n=\frac{3}{4}・(-1)^{n-1}+\frac{5}{4}・3^{n-1}$$
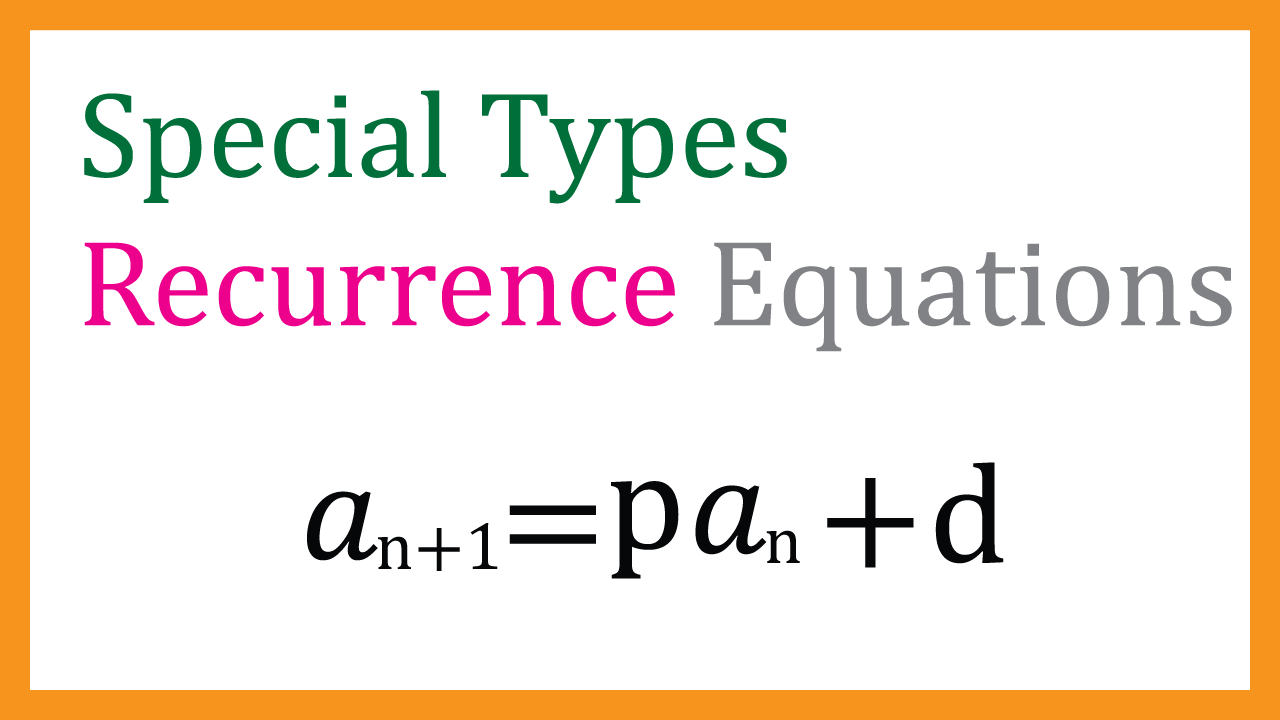
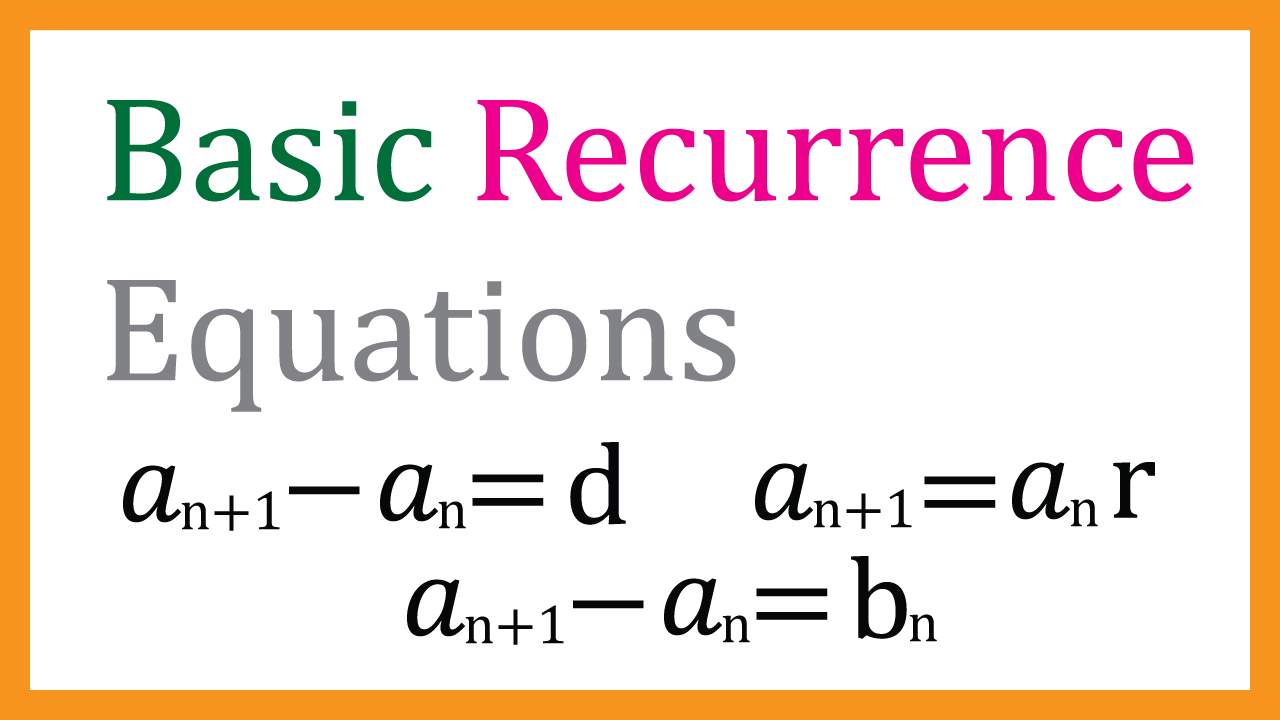

コメント