
相対性理論という名前
宇宙のことを考えたときに「相対性理論」って言葉が頭に浮かぶかもしれない。浮かばないかもしれない。いや、思いつくいろいろな名前の中のひとつには入っていると思う。
アインシュタインが提唱したっていうのは分かっているけど、実際何のことかはわからない人も多いのではないか。
何、何?相対性?何で宇宙のことなのに相対性?相対?なんか、あなたと私、みたいな感じに聞こえる。
物理っぽくない名前。
その感じすごくわかる。僕も同じこと考えてた。
だってさ、他の物理学の名前には「力学」とか「電磁気学」とか「量子力学」とかいかにもな名前が付けられている。
なのに相対性理論ってなんか、こいつだけ違う?
だけど
実はこのネーミングって結構合ってて、本当に相対性理論はあなたと私の状態について考えましょうっていう部分もあるようだ。状態っていっても、暑い寒いとか、気分が良い悪いっていう話ではなくって、あなたと私のいる場所とか、速さとか、時間とか、そういったものだ。
え、それって、めっちゃ身近なことちゃう?
物理の1番初めに勉強するやつ。
もしかしたら物理じゃないかもしれない。算数とか数学で学ぶかもしれない。
相対性原理
\(時速50km\)で走っている車と\(時速100km\)で走っている電車があるとする。僕がそれらを地面に立って眺めているときはそれらの速さはそのままだ。
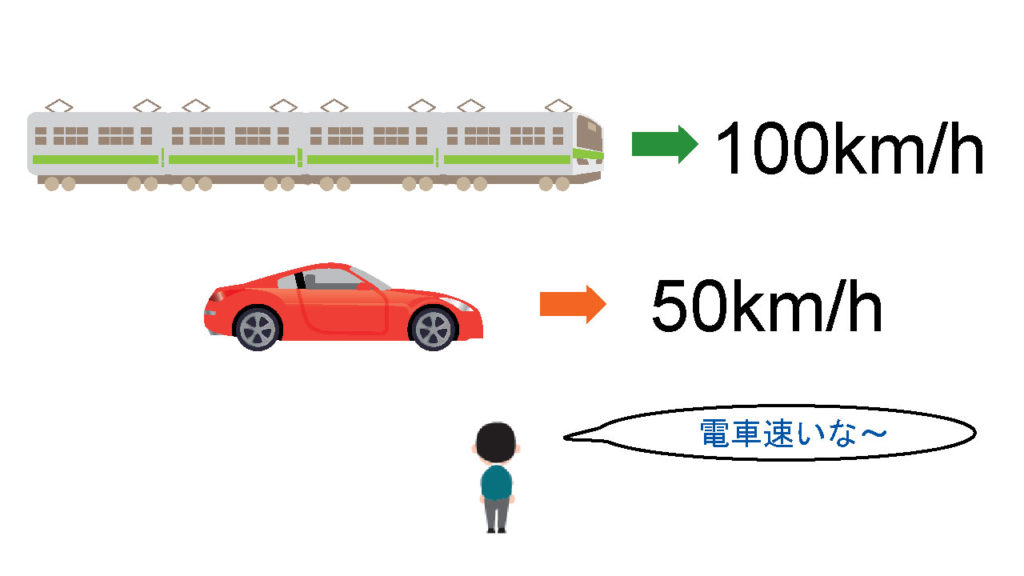
しかし、僕がその\(時速50km\)で走っている車に乗ると、\(時速100km\)の電車は
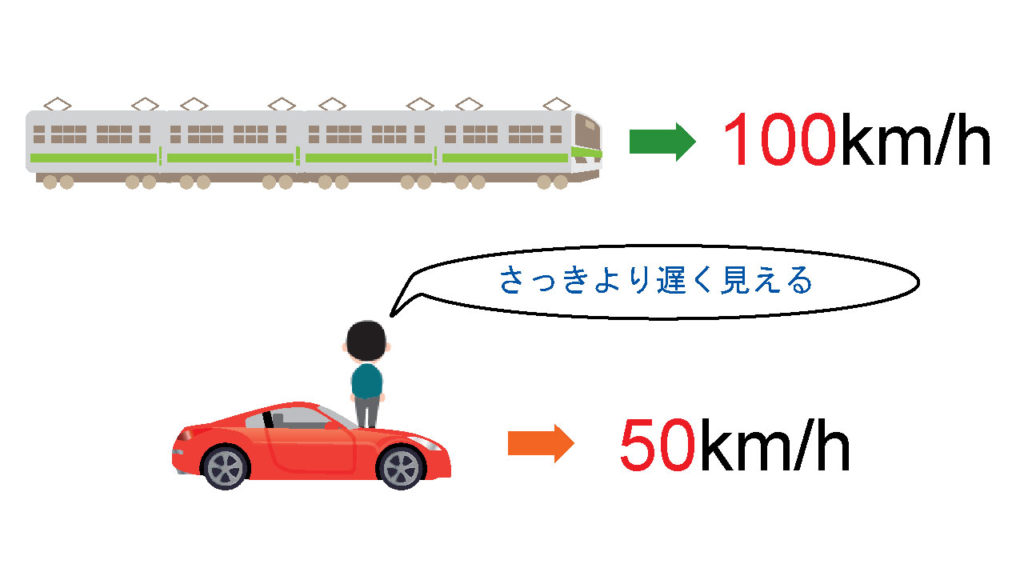
$$時速100km\ –\ 時速50km\ =\ 時速50km$$
つまり、車に乗って電車のほうを見ると、\(時速50km\)で走っているように見えるのだ。
「それは実際の速さじゃないやん」と言われるかもしれないけど、そもそも僕たちが静止していると思っているこの地面、つまり地球も、太陽の周りを回っていることになっているので、静止している場所を探すのはかなり難しいのだ。しかし電車も車も我々人間も、まあまあの速度で動いている地球の上にいるので同じシステムの上で動いている。後で説明するが、これを同じ慣性系にいるという。
ちなみに宇宙は加速しながら膨張していると言われているから、なおのこと止まっている場所というものを見つけるのは不可能のように思える。
何が言いたいかというと「全ては相対的だ」ということである。
要は自分のいる場所、あなたの場所、それから速さなんかというものは、すべてあなたとか私の関係性の中でしかわからないということだ。
ああ!なるほど!それで「それで“相対性”か!」それがアインシュタインの言ったことだったんだ!意外とかんた…
いや、残念だが、さすがにそこまで簡単じゃない。
相対性理論っていうのは、この考え方をもとに作られたかもしれないけど、これは相対性理論じゃない。
ややこしいかもしれないけど、これは相対性原理と呼ばれているものだ。
じゃあ相対性理論って何?
それじゃ、アインシュタインの相対性理論(原理じゃないよ)とは何か。
かなりざっくり言えば、光について考える学問と言える。これは本当にざっくりだから、何となくのイメージを持ってもらいだけだ。
光の速さがとてつもなく大きいのは良く知られている。カミナリが落ちると、音よりも早くカミナリの光がこちらに届くし、光が1秒間に地球を7周半するってのは聞いたことあると思う。
その光の速さというのは、さっきの相対性原理が正しいのであれば、光の速さも足したり引いたりして表すことができるはずである。
さきほどは、走っている車の中から隣を走る電車を見ると、地面に立っていた時よりも遅く見えることを話した。
次は、もし車が\(時速100km\)で走っていれば、同じく\(時速100km\)で走っている電車は車に乗ってる僕らからは止まって見える。この辺は、一度でも車や電車に乗って、となりを走る車両を見たことがあればイメージしやすいと思う。
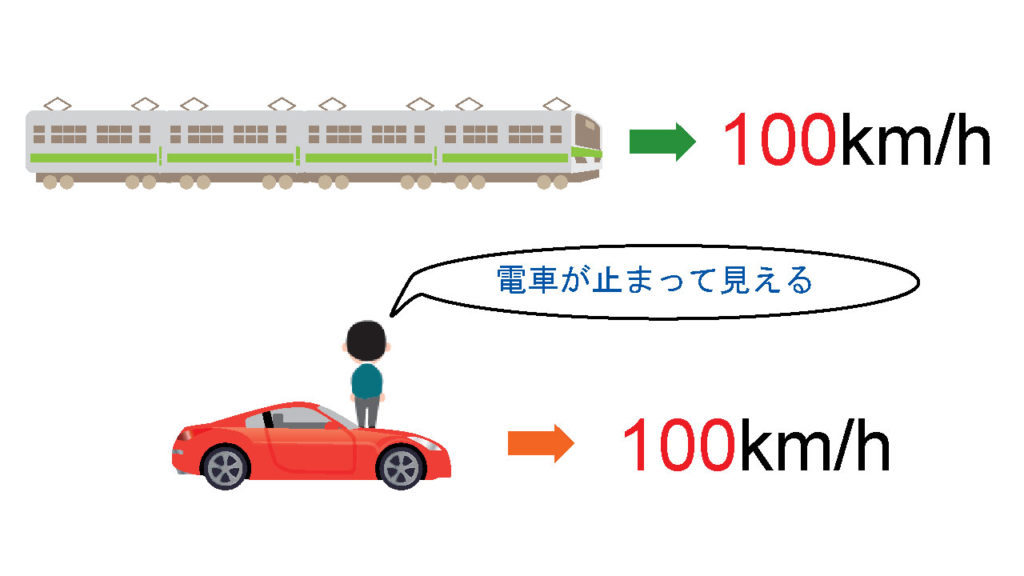
思考実験
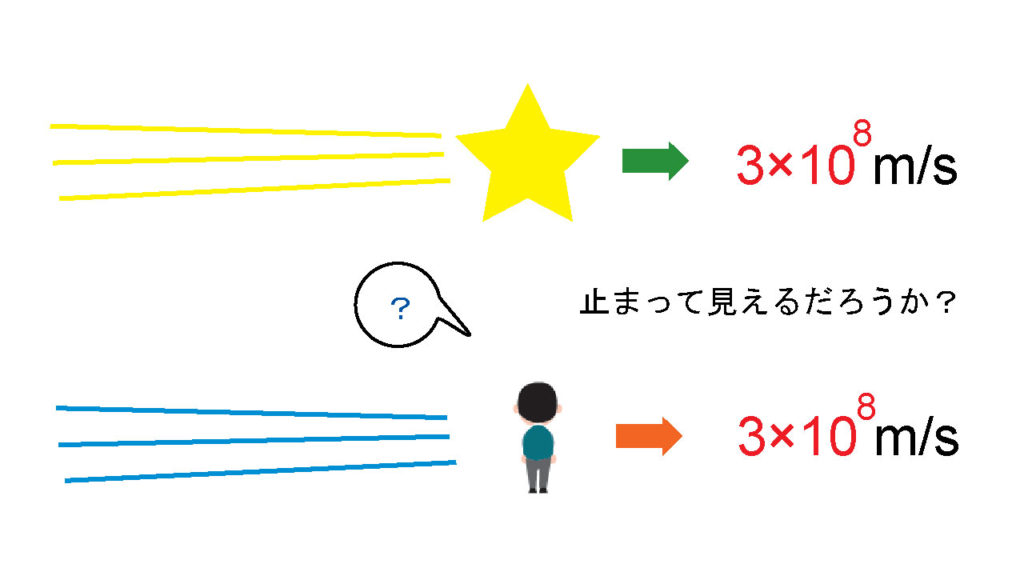
そこからアインシュタインは頭の中で「じゃあ。光の速さで光のそばを走ったら、その光は止まって見えるのだろうか」と考えた。もちろん実際に光の速さで移動することは不可能だし、それに近い速さで人間が移動することもめっちゃ難しいだろう。しかし頭の中で考えるのは自由だ。これを思考実験と呼ぶ。
光について考えると、いろんなことが不思議に思えてくる。詳しくは話さないけれど、光について理解できたら、この世界の仕組みがもっとよくわかるような気がする。
さっきの思考実験もそうだけど、次のやつもおもしろい。
例えば大きな大きな部屋があるとする。そして天井はものすごく高く、\(15万km\)あるとする。それはうまいこと、床から放たれる光が天井の鏡に反射して、ちょうど1秒で往復して帰ってくる距離になっている。光が1秒間に進む距離は\(30万km\)だ。
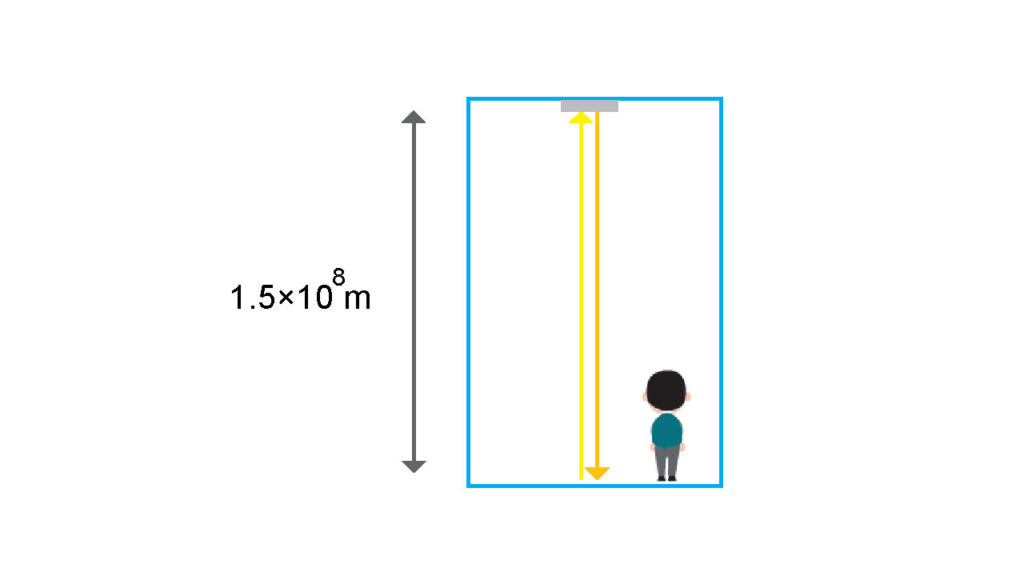
さらに、その大きな部屋は横に一定のスピードで移動するとする。
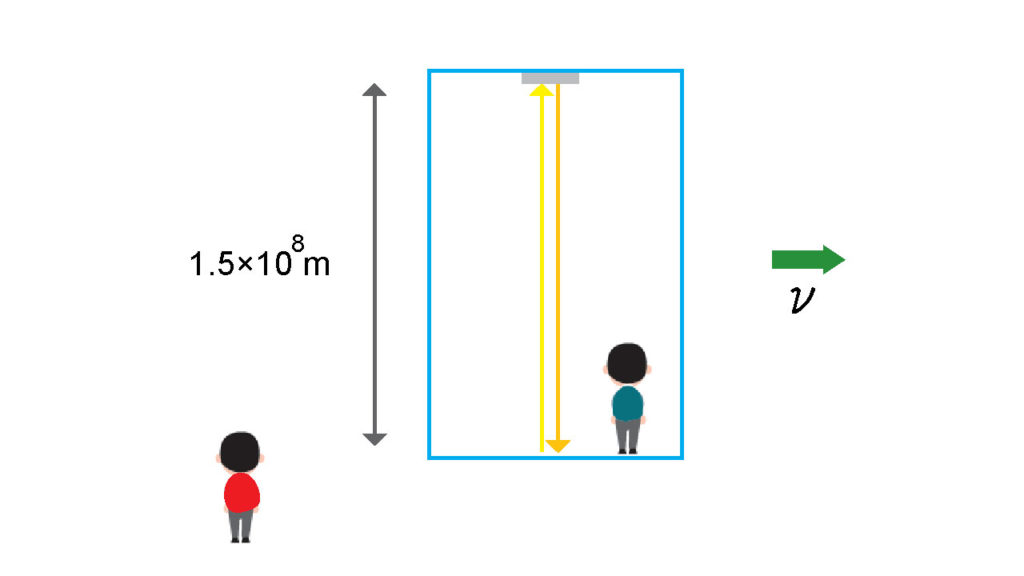
さて、どうなるだろう。
部屋の中にいる青い人には何も問題ない。そのレーザーが床から発射されて、その\(0.5秒後\)に天井の鏡に反射し、1秒後にもとの床に帰ってくる。いつも通りの結果を目にする。
しかし、それを部屋の外から見ている赤い人には、その光の進み方はどのように見えるだろうか。幸いなことに、その部屋の壁は透明で、外からでも光の軌跡が見えることになっている。これは思考実験なのだから、自分の好きなように設定できるのだ。
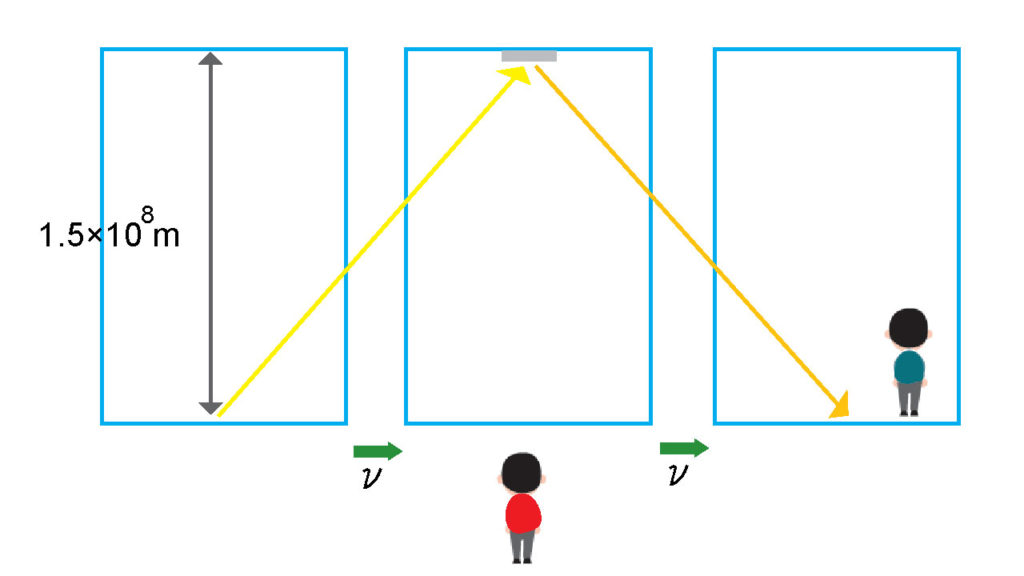
部屋は横に移動しているのだから、部屋の中で見るように真上に光が行って帰ってくるのとは様子が違う。横に移動したことで、光の軌道が斜めになって、光が辿った道のりは長くなっている。灰色の矢印と黄色の矢印の長さを比べてみると差は歴然だ。部屋の中の青い人にとっては、光が往復\(30万km\)の距離を進んだのだから、同じ\(1秒\)の間に起こったことのはずなのに、である。
これをどう説明すればいいのか。可能性はいくつかある。
1.光の速さが動いているエレベーターの中で速くなった。
2.動いているエレベーターの中の時間の進み方が遅くなった。
相対性理論によれば、2の「動いているエレベーターの中の時間の進み方が遅くなった。 」を正解とする。変化したのは時間の進みぐあいなのだ。
なぜ光の速さではなく、時間が伸び縮みすると考えるのか
ここは少しわかりにくい部分かもしれない。
というのも、明確に理由があって時間の伸び縮みする方を選択するのではなく、光の速さが慣性系によらず一定であるというのが、相対性理論(正確に言えば特殊相対性理論)の基本原理のひとつだからである。この基本原理という設定をもとに相対性理論を組み立てたのだ。
「慣性系によらず」の文言がわからない人がいるかもしれない。さっきの例でいえば、動いているエレベーターの中にいる青い人と外にいる赤い人とでは「慣性系が違う」と物理では表現する。
同様に、地面に立って動いている乗り物を見ている人と、乗り物に乗っている人とでは慣性系が違う。本来は、慣性系が違えばそれぞれが感じる乗り物の速度は違って見えるはずなのだが、光だけは特別で、慣性系に限らず(自分が乗り物に乗っていようがなかろうが)どんな状況でも光の速さは一定である、という考えをもとに理論が作られている。
順序立てて、こうだからこう、という論理ではなく「光の速さは慣性系によらず一定」として組み立てたら観測の事実と一致した、という具合だ。アインシュタインも理論を組み立てた当初は、それが正しいという証拠はなかっただろうが、ある種の確信をもって取り組んでいたに違いない。
マイケルソン・モーリーの実験
「光の速さが慣性系によらず一定」の完全な証拠にはならないようだが、それをサポートする有名な実験がある。それがマイケルソン・モーリーの実験だ。
当時は、もちろん相対性理論は完成していなかったが、光の速さがどうやら有限であることがわかっていた。というのも光は速すぎて、それを計ることは昔の人にとっては難しかったのだ。しかし、レーマーという人のおかげで、「光の速さが有限」であることがわかり、さらにヤングの干渉実験から「光には波の性質がある」ことがわかり、そこからまた新しい疑問が浮かび上がった。
それは「光は何を媒体にして伝わっているのだろう」という疑問だ。
波の性質を持つ他の身近なものといえば、音だ。音は約\(340m/s\)の速さで空気などを媒体にして進む。そのことから光も何かを媒介して伝わっているはずだと当時の科学者たちは考えた。そこで考え出されたのが、エーテルというものだ。
ある有名なゲームの中にMP(マジックパワー)を回復するアイテムとして登場するが、本来のエーテルにはそんな効果はない。効果がないどころか、奇妙なほど希薄で透明で化学的に不活性な存在なのだ。
ともかく当時の人は、エーテルの存在を信じたのだ。
ボートで川を往復するとどうなるか
マイケルソン・モーリーの実験を理解するために、まずは川をボートで漕ぐ状況を考えよう。ボートを漕ぐ人は川のように流れのない水の上で\(5(m/s) \)の速さで漕ぐものとして、川の水の流れは上流から下流に向かって\(3(m/s) \)とする。
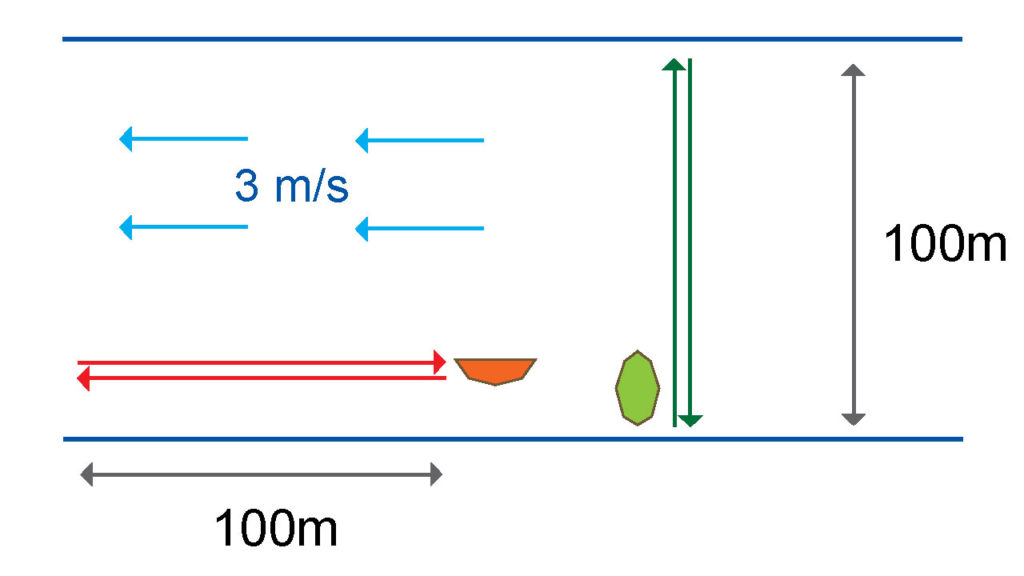
ひとりは川を下流に向かって(川の流れに乗って)\(100m\)進み、そして戻って(流れに逆らって)くる。図の赤の矢印だ。
もうひとりは川の対岸に向かって(川の流れを横切って)同じく\(100m\)進み、戻って(川の流れを横切って)くるとする。図の緑の矢印だ。
はたして同じ\(200m\)を漕ぎ終わる時間に違いは出るのだろうか。
川の流れに沿って漕いだ赤いボートの時間
下流に向かう時の速度
$$v_l=5\left(\frac{m}{s}\right)+3\left(\frac{m}{s}\right)=8\left(\frac{m}{s}\right)$$
下流に向かって\(100m\)漕ぐのにかかる時間
$$t_l=\frac{100(m) }{8(m/s)}=\frac{25}{2}(s)$$
上流に向かう時の速度
$$v_u=5(\frac{m}{s}) -3(\frac{m}{s}) =2(\frac{m}{s})$$
上流に向かって\(100m\)漕ぐのにかかる時間
$$t_u=\frac{100(m)}{2(m/s)}=50(s)$$
トータルでかかる時間
$$t_l+t_u=62.5(s)$$
である。
川の流れを横切って漕いだ緑のボートの時間
川は常に水が\(3(\frac{m}{s}) \)という速さで流れている(水色の矢印)から、ボートを漕ぐ人は少し上流に向けて(黄色の矢印)漕がなければ真っすぐ対岸に向かって(緑の矢印)進めない。
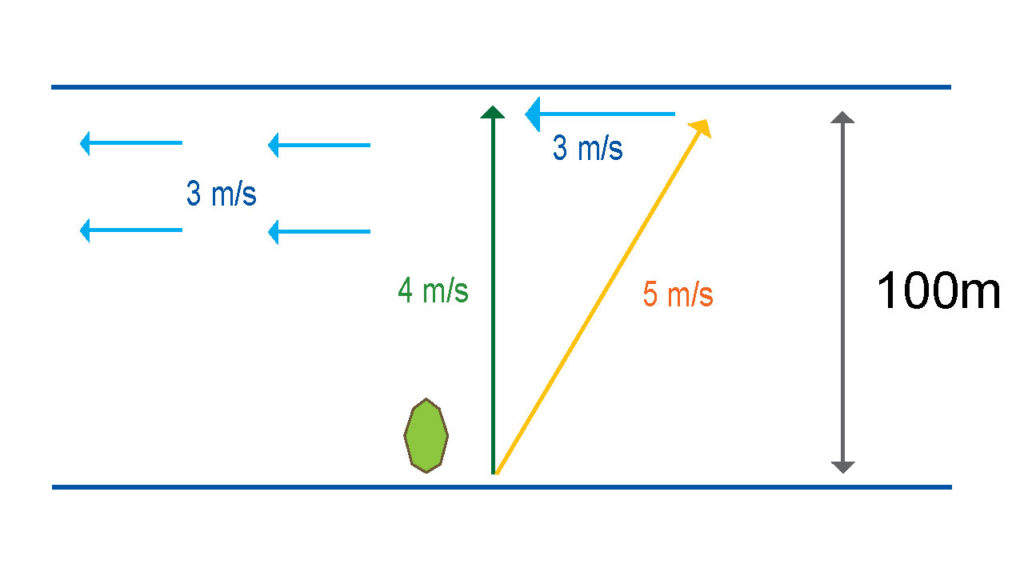
ピタゴラスの定理から結局\(4(\frac{m}{s}) \)という速度で川を渡ることになる。行きも帰りも速さは変わらないのでトータルでかかる時間は
$$\frac{200(m) }{4(m/s)}=50(s)$$
となり、川の水の流れに沿って(赤い矢印で)漕ぐか、横切って(緑の矢印で)漕ぐかで時間に差が出た。
この事実を踏まえて、エーテルについても考えよう。
先ほどエーテルは奇妙なほど希薄で透明で化学的に不活性な存在といったが、エーテルが川の水のように流れているのなら、それを媒体とする光の速さにも違いが出るはずだと考えたのだった。流れを作るのはそう難しくない。例えば風の全く吹いていない日でも、自ら走ることで風を感じることができる。年を取ってしまったが、僕も昔は風を切ってサッカーグラウンドを走り回っていたものだ…
Anyway
地球は太陽の周りをまあまあの速度で周回しているので、僕らが走っているときに風を感じるようにエーテル風というものが発生しているはずなのだ。そこでマイケルソンとモーリーはこのような装置を作った。
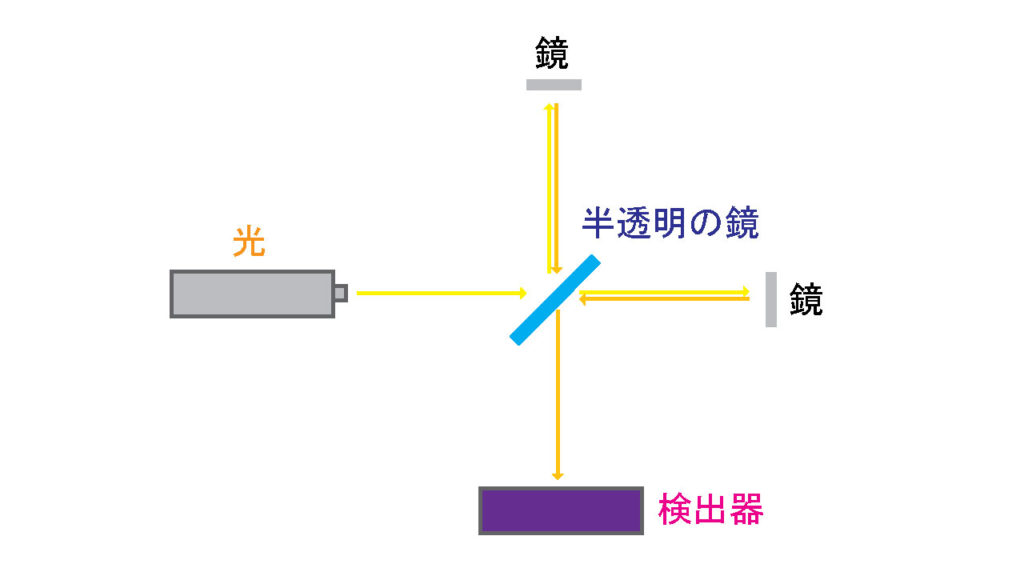
中心にあるものは半透明な鏡で、光を真っすぐ進むものと\(90°\)屈折させて進むものの2つに分ける。真っすぐ進んだ光が鏡に反射して帰ってきたものと、屈折して進んだものが帰ってきたものを同じように半透明の鏡を使って検出器に入れる。
もしエーテルの風の影響を受けているのなら、光が半透明の鏡を通過して、真っすぐ進んだり屈折して進んだりしている間に、戻ってくるまでの時間に変化が現れるはずである。
しかし、実験の結果にはエーテルの風の影響を受けていると言えるほどの違いはなかったようだ。
アインシュタインはこの実験のことを知らずにエーテルは存在しないだろうと自らの思考実験で導き出していたし、「光の速さはどんな慣性系でも同じ速度である」を基本原理とした相対性理論はさまざまな観測事実と一致することになり、いかにアインシュタインがすごいのかがわかるだろう。
物理は感覚と事実の違いを教えてくれる
「え!?時間ってみんな平等に流れているんじゃないん!?」
と思うかもしれない。そのコメントにはごもっとも。僕も大変驚いた。
時間の流れこそ、全宇宙共通のものだと思っていたけれど、相対性理論ではどうやらそうではないのだ。
先ほどの大きな部屋の例でいうと、動いている部屋の中で進む時間の速さは、外から見ている人に比べて、光の移動距離が長くなった分、遅くなるということだ。
僕らが絶対的な基準だと思っていた時間というのは、どうやら地球上だけでの話のようだ
ポイント:時間は絶対ではなく、光のスピードが絶対的基準
もちろん、この思考実験だけで、相対性理論が完成したわけじゃない。
でも相対性理論のアイデアとしては、これだけでもなんとなく理解できたはず。
ただ僕らが住んでいる地球の表面では、その時間が遅くなったりすることはなかなか確認できないようだ。普段、僕らが普段扱っているスピードというのは、時間が遅くなったりするには小さすぎる。
例えば、GPSは地球の周りを回っている人口衛星からの情報を頼りに機能しているのだが、人口衛星はある程度のスピードをもって移動しているので、相対性理論を考慮しないとGPSがうまく機能しないと言われている。
そう言ったことから相対性理論は、宇宙に関する理論というよりは、もっと大きな視点で物事を見るための理論だと言える。
僕たちが高校生までで勉強する物理はニュートン力学と呼ばれているけども、相対性理論はその扱うスケールが大きくなっても通用する理論だ。
決してニュートンが間違っていたということではない。扱うスピードが光の速さに比べて小さいときは、ニュートン力学で十分というか便利なのだ。




コメント