曲率（K）とは何か

なぜ曲率（K）？

前回、フリードマン方程式を紹介したときに、ひとつ説明しきれていないことがあった。

$$ \left( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3} \rho -\frac{\color{red}{K}{c^2}}{a^2} $$

それは右辺第２項にある$K$で表された曲率だ。なんとなく言葉のイメージはつかみやすいと思うが、これは曲線や曲面がどの程度カーブしているかという曲がり具合を示している。

下の図を見てほしい

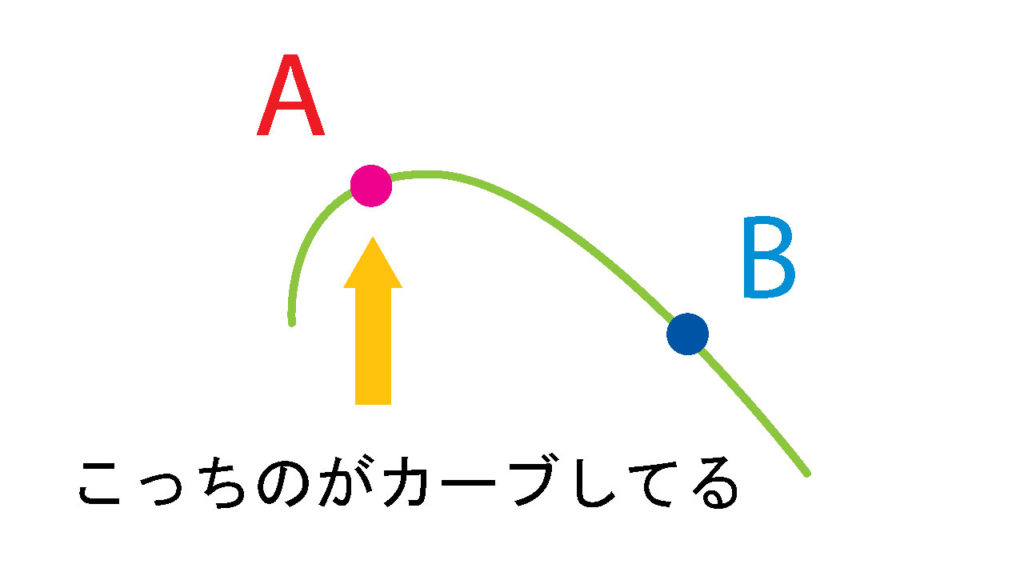
AとBを比べてみると、A付近の線の方がよくカーブしているのがわかる。よってこちらの方が、曲率が大きいはずだ。

さてどのように定義するのか。

曲線の２点の接戦を下の図のように描いて、このとき作り出される角度が大きければ大きいほど、曲線の曲がり具合が大きいといえる。この状況の２つの点を限りなく近づけていったときの「２接戦のおりなす角と弧ABの長さの比の値」を曲率とされている。

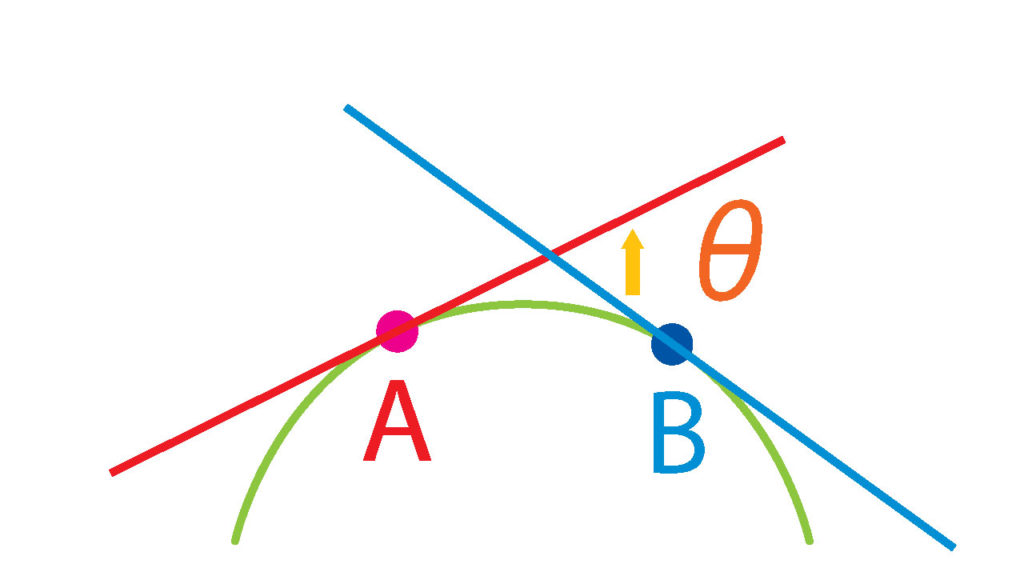
$$K=\lim_{B\to A} \frac{\theta_{AB}}{l_{AB}}$$

ちなみに、曲率Kの逆数はその曲がり具合で描かれる円の半径になっている。

それでは、そもそも何故曲率という概念が必要なのだろうか。

紙の上での曲率の話はわかりやすい。曲線を描いた曲がり具合のことだから、とてもイメージしやすいし、何となくだけど理解できると思う。

しかしそれらは、ある意味特殊な（限定的な）状況であることを理解していなければならない。専門用語を使えば、それはユークリッド幾何学と呼ばれている。

名前を聞くとたいそうなネーミングと感じるけども、これは普段の算数や数学で使われている今まで通りの図形の取り扱いの話である。「２本の平行な直線は決して交わらない」とか「三角形の内角の和は１８０°」だとかである。

しかし、宇宙を学んでいくにあたって、これからは非ユークリッド幾何学というものを取り扱っていかなくてはならない。これはもっと一般的（不偏的）な状況の中での幾何学である。

この状況下では、たとえ紙の上に完ぺきな平行な２本の直線を描いたとしても、その紙自体が歪んでしまっていれば、その２本の線は曲線になってしまうということが起こりうる。

世界地図と地球儀を思い浮かべるとわかりやすいかもしれない。縦に引かれた水色の線を経度、オレンジの線を赤道だとすれば、下の図のようになる。限りなく簡略した図だ。

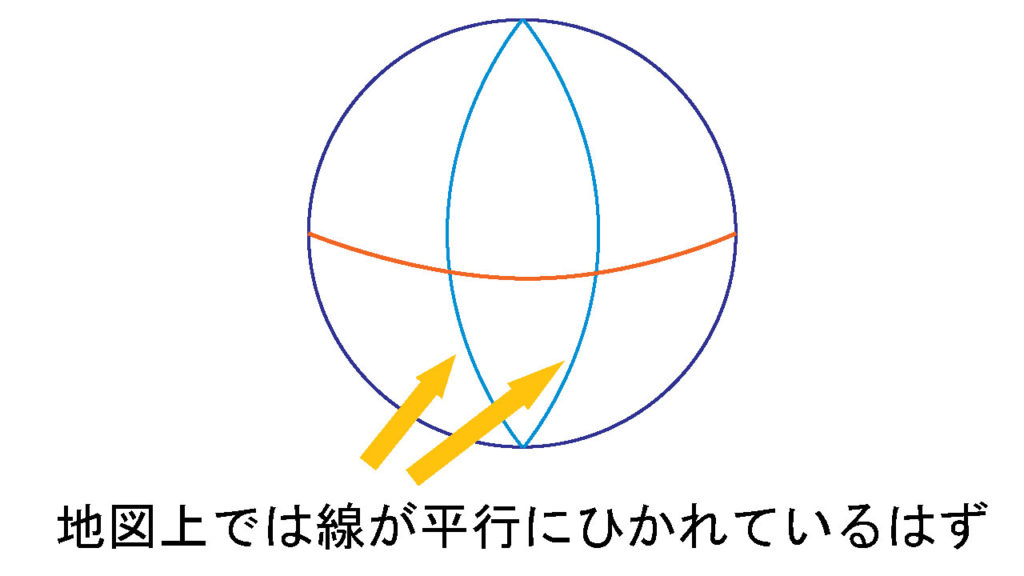
机の上に広げられた世界地図上では、経度は上下（南北）に平行な線で描かれている。しかし、地球儀を見てみると、その経度は北極と南極で交わってしまっている。上で述べた通り普段の図形の問題では、平行な２本の線は決して交わらないというのが鉄則だが、これはユークリッド幾何学（世界地図）の話だったのだ。しかし、非ユークリッド幾何学（地球儀）では、また違った原則があるようだ。

ここから、曲面の曲率の求め方を学んでいくべきなんだけれども、それは少しややこしいので、別の機会に書くことにするけども、何となく空間の曲率というものが宇宙を勉強する上で大切かというのがわかったと思う。

もし空間が歪んでいれば、これまでの幾何学の考え方を改めなければならないのだ。