Why Is Harmonic Series the Divergent Infinite Series

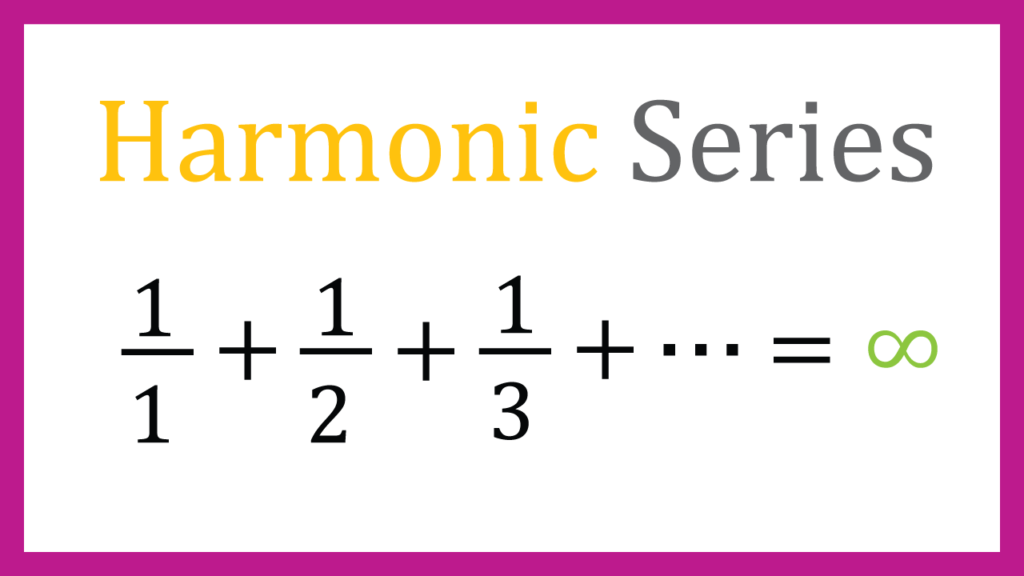
By the way what is Harmonic Series??

$$\sum^{\infty}_{n=1}\frac{1}{n}=\frac{1}{1}
+\frac{1}{2}
+\frac{1}{3}
+\frac{1}{4}
+\frac{1}{5}+・・・ $$

This is called Harmonic Series.

We have 2 kinds of series, convergent and divergent. Divergent series means that the sum of all sequences would go to infinity. On the other hand, convergent series would have a specific number if you add all terms.

At a glance, this Harmonic series is thought to be convergent since the value of the fraction is going to be smaller and smaller as the number of the term increases.

However, let me tell you the result first, Harmonic series is divergent.

Here is how we know it.

$$\sum^{\infty}_{n=1}\frac{1}{n}=\frac{1}{1}
+\frac{1}{2}
+\frac{1}{3}
+\frac{1}{4}
+\frac{1}{5}
+\frac{1}{6}
+\frac{1}{7}
+\frac{1}{8}
+\frac{1}{9} +・・・ $$

It would be hard to consider of itself for understanding the series.

Now we use a typical way to analyze series. That is to introduce another series which is slightly smaller than Harmonic series.

$$\frac{1}{1}
+\frac{1}{2}
+\frac{1}{4}
+\frac{1}{4}
+\frac{1}{8}
+\frac{1}{8}
+\frac{1}{8}
+\frac{1}{8}
+\frac{1}{16} +・・・ $$

Please compare 3, 5, 6, 7, 9th terms for each series. New ones are definitely smaller than Harmonic ones, aren’t they.

Then let’s put some parentheses so that you could see the result.

$$\frac{1}{1}
+\frac{1}{2}
+\bigg(\frac{1}{4}
+\frac{1}{4}\bigg)
+\bigg(\frac{1}{8}
+\frac{1}{8}
+\frac{1}{8}
+\frac{1}{8}\bigg)
+\bigg(\frac{1}{16} +・・・ $$

$$=\frac{1}{1}
+\frac{1}{2}
+\frac{1}{2}
+\frac{1}{2}
+\frac{1}{2} +・・・ $$

$$=\infty$$

If you add \(\frac{1}{2}\), \(0.5\) forever, it definitely goes to \infty.

Even this new series which is smaller than Harmonic series goes to infinity(divergent), Harmonic series must go to be divergent, as well.

This result is opposite to our intuition.